One of previous posts presented partitioning strategies. Among described techniques we could find hashing partitioning based on the number of servers. The drawback of this method was the lack of flexibility. With the add of new server we have to remap all data. Fortunately an alternative to this "primitive" hashing exists and it's called consistent hashing.
Data Engineering Design Patterns
Looking for a book that defines and solves most common data engineering problems? I'm currently writing
one on that topic and the first chapters are already available in π
Early Release on the O'Reilly platform
I also help solve your data engineering problems π contact@waitingforcode.com π©
This post explains the idea of consistent hashing defined in Dynamo paper (link in the section "Read also"). The first part introduces this concept from the theoretical point of view. Next we'll focus on Dynamo implementation showing 3 tested strategies to handle even load between nodes. The last part shows a simple implementation of consistent hashing ring.
Consistent hashing definition
One of partitioning strategies is modulo-based partitioning. The data partition is computed from a simple formula of hash(object) % numberOfNodes. It performs pretty well when the numberOfNodes doesn't change. When it's variable, the big problems of modulo-based partitioning appear. Among others, with every change in the cluster (added or removed node) the hash of all elements must be recomputed and these elements must be moved to new locations. In the context of heavy load, it can be very consuming operation.
To cope with this issue a lot of work was done and one of approved solutions was consistent hashing. It represents the data in the form of a circle where each node is represented by a point. By doing so, each node is responsible for the data between it and its predecessor, as illustrated in the following image:
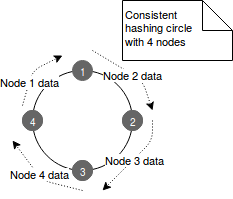
Now if one of nodes is removed, only the data held by it must be remapped. The same rule applies for a node joining the cluster. The new node takes the place between 2 already existent ones and only the data from this chunk must be remapped. To resume, only k⁄n keys are remapped where k is the number of keys and n the number of nodes.
One of the potential problems of above implementation is the fact that some ranges can be more loaded than the others. A solution for that is the use of virtual nodes that guarantee more fine grained presence of the nodes in the circle. In fact each node is assigned to multiple points in the circle called virtual nodes. Physically they all point to the same machine and conceptually they help to distribute the data more evenly. The following image illustrates that:
Thanks to the idea of ring the algorithm used to find the virtual node responsible for given key is straightforward and it can be resumed in the following 2 steps:
1. hash(key) - defines item's position in the ring 2. Walk clockwise in the ring - the first node with the position larger than item's position is the node storing given item.
Dynamo load strategies
One of challenges in consistent hashing ring is the even distribution of the data. The paper "Dynamo: Amazon's Highly Available Key-value Store" makes an insight on 3 strategies implemented in different time in Dynamo key-value store to improve data load balancing in the case of data replicated on N nodes:
- Strategy#1 - each node has assigned T tokens in random manner. Because of the randomness the ranges can have different sizes. The problem with this approach occurs when a new node joins the cluster. The new node takes already occupied tokens. Because of that the "old" nodes must scan their local storage to retrieve the "stolen" data and send it to the incomer. For instance let's imagine a node A responsible for range (1, 5], node B for range (5, 10] and node C responsible for range (10, 20]. A new node D is added to the cluster and it takes the ranges (4, 8]. Further to that, the A and B nodes scan their local storage to retrieve the items to transfer to the node D.
The other point of difficulty was the archival process. Archiving entire key space required each node to retrieve all archived keys locally, exactly as in the case of data distribution, through heavy scan operation. The following image shows a possible ring state for this strategy:
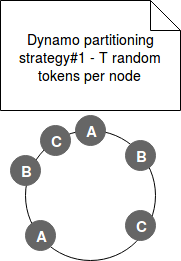
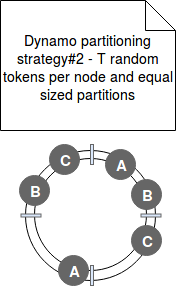
- Strategy#2 - this strategy was an intermediary state in transition from the previous to the next strategy. In Strategy#2 each node has still T randomly chosen tokens on the ring but the hash space changed. It's now composed of equally sized partitions (ranges).
Moreover, unlike previous strategy, the data partitioning and data placement schemes are decoupled. The hashing function (partitioning) is only used to map values in hash space to the ordered list of nodes. The data is placed independently on that - on the first N nodes encountered while walking the ring from the end of the partition that contains saved key (because data must be replicated in N different nodes):
- Strategy#3 - this final strategy is based Q/S tokens per node (Q - number of partitions, S - number of nodes) with still equally sized partitions. It's similar to the previous strategy but the difference is that with each token's redistribution (= added or removed node), the property of Q/S tokens per node is preserved:
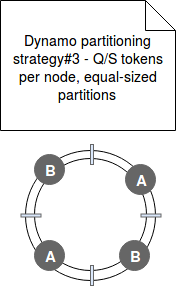
After the tests the last strategy appeared to be the right one. Firstly, the partition ranges are fixed and because of that they can be stored in different files. Now, when the data must be remapped, the impacted file is simply copied to new node. There is no need to random access and heavy scan operation. Secondly, the archiving process is simplified. It's related to the previous point - scanning data is not required and the snapshot of given partition represents the content of the file at given moment.
Thanks to this 3rd strategy we can also tell what happens when the cluster changes. If new node appears in the cluster it "steals" the virtual nodes (tokens) from the ring. The nodes holding the data from stolen points transfer the appropriated files to new node. When a node leaves the cluster, the same operation occurs but in reverse order. The node leaving the cluster evenly distributes its virtual nodes and stored data to the remaining nodes. Both operations preserver Q/S property introduced in the Strategy#3.
Consistent hashing example
In the consistent hashing ring we could adopt 2 discovery strategies: store somewhere a map between range and nodes or use clockwise walk to find the node matching given hash key. The first strategy performs well on searching (O(1)) but requires more storage (O(n) where n is the number of ranges). The second strategy has reversed characteristics: searching is O(n) and the storage is O(1). The example of their implementation is shown in the following code snippet. Please notice that it shows the simplified version of the ring without the ideas of virtual nodes and equal-sized partitions:
class ConsistentHashingTest extends FlatSpec with Matchers {
"clockwise ring" should "find the node for hashed key in the middle of the ring" in {
val node5 = ClockwiseNode(None, 5)
val node4 = ClockwiseNode(Some(node5), 4)
val node3 = ClockwiseNode(Some(node4), 3)
val node2 = ClockwiseNode(Some(node3), 2)
val node1 = ClockwiseNode(Some(node2), 1)
val clockwiseRing = ClockwiseRing(node1)
val matchingNode = findNodeForHash(3, clockwiseRing)
matchingNode shouldEqual node4
}
"clockwise ring" should "find the node for hashed key on the beginning of the ring" in {
val node5 = ClockwiseNode(None, 5)
val node4 = ClockwiseNode(Some(node5), 4)
val node3 = ClockwiseNode(Some(node4), 3)
val node2 = ClockwiseNode(Some(node3), 2)
val node1 = ClockwiseNode(Some(node2), 1)
val clockwiseRing = ClockwiseRing(node1)
val matchingNode = findNodeForHash(0, clockwiseRing)
matchingNode shouldEqual node1
}
def findNodeForHash(hash: Int, clockwiseRing: ClockwiseRing): ClockwiseNode = {
var node = clockwiseRing.firstNode
var targetNode: Option[ClockwiseNode] = None
while (node.successor.isDefined && targetNode.isEmpty) {
if (node.startRange > hash) {
targetNode = Some(node)
}
if (node.successor.isDefined) {
node = node.successor.get
}
}
targetNode.get
}
"map-like ring" should "find the node for hashed key" in {
val node1 = MapLikeNode(1)
val node2 = MapLikeNode(2)
val node3 = MapLikeNode(3)
val mapLikeRing = MapLikeRing(Map(1 -> node1, 2 -> node2, 3 -> node3, 4 -> node1, 5 -> node2, 6 -> node3))
val hashKey = 3
val targetNode = mapLikeRing.nodes(hashKey)
targetNode shouldEqual node3
}
}
case class ClockwiseRing(firstNode: ClockwiseNode)
case class ClockwiseNode(successor: Option[ClockwiseNode], startRange: Int)
case class MapLikeRing(nodes: Map[Int, MapLikeNode])
case class MapLikeNode(id: Int)
Consistent hashing is a remedy for the problems brought with the modulo-based hashing. Certainly, it doesn't eliminate the requirement to move the data when a node joins or leaves the cluster. But thanks to the more flexible distribution of data only a small subset of the data must be moved. As shown in the example of DynamoDB in the 2nd section, the consistent hashing is also useful in the context of replicated database. Among 3 placement and partition strategies, the last one based on equal sized partitions and even distribution was judged the most efficient for the needs of this data store. And the last part presented 2 possible implementations of nodes discovery: map-based and clockwise.
