Bloom filter has a lot of versions addressing its main drawbacks - bounded source and add-only character. One of them is Scalable Bloom filter that fixes the first issue.
This post begins by an explanation of Scalable Bloom filter theoretical points. In the second part it focuses on the implementation side. The last section contains some tests with the help of Python's python-bloomfilter library.
Definition
To work properly basic Bloom filter version must know the number of elements in the dataset. However this requirement is not always possible to fulfill. It's the case of data coming from unbounded data source, as for instance a stream. To deal with such kind of values with basic Bloom filter we need to overestimate the filter's size and monitor its fulfillness that after reaching some threshold would inevitably lead to the creation of new and much bigger Bloom filter. And generally that's the idea adopted by Scalable Bloom filter. Instead of working with one and big filter, it creates several different filters with increased capacity. It's summarized in the following image:
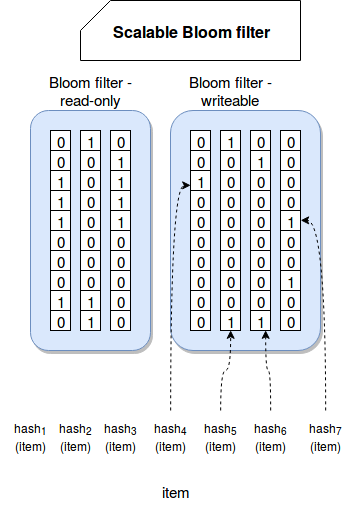
As you can see, when the filter reaches some fulfillness threshold, it becomes read-only and new bigger and writable filter is created in its place. If in its turn it becomes saturated, the operation is repeated. Every new filter, in order to keep the false positives rate close to the targeted one, has more hash functions than the previous filter.
In Scalable Bloom filter the membership test is applied on all created (read-only + writable) filters. If the item is missing in all filters, it's considered as not existing. In the other side, if one of the filters reports its existence, it means that the element may be in the dataset. An important point to notice here is that Scalable Bloom filter uses a variant of Bloom filters where the bit vector is divided in k slices where each stores M/k bits (M is the size of whole bit vector). Since the number of slices is equal to the number of hash functions, each hash function works on its own slice:
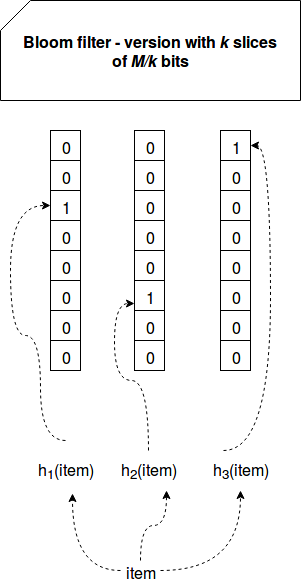
Thanks to the slices each element is always described by k bits resulting on more robust filter without the elements more prone to the false positives than the others.
Scalable Bloom filter can grow indefinitely. Because of that it's a good suit only for the places where the memory constraint doesn't exist. Otherwise any of other alternatives as Stable Bloom filter, covered in one of further posts, should be envisaged.
Implementation
What is the logic behind growing filters ? The Scalable Bloom Filters paper quoted in "Read also" section gives some insight about the parameters to chose. According to it a good factor for growth scale (= how many times new filter will be bigger than the current one) is 2 when the growth is slow or 4 where it's fast.
Scalable Bloom filter introduces also another important parameter called tightening ratio. Thanks to it every new filter will have smaller false positives ratio than its precedesor. It guarantees that the overall false positives ratio will be close to the global expected ratio. According to the paper a good tightening ratio is between 0.8 and 0.9. The false positives ratio for a particular filter is computed as:
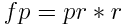
Where pr is the false positives ratio of previous filter and r is the tightening ratio. The formula used to compute the false positives ratio of the first filter is a little bit different:
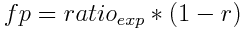
Where ratioexp is the expected global false positives ratio. Everything can be easily tested for a finite number of iterations (growths):
>>> r = 0.9 >>> expected_ratio = 0.05 >>> ratios = [ (expected_ratio * (1.0 - r)) ] >>> ratios [0.004999999999999999] >>> for previous_ratio_index in range(0, 20): ... ratio = ratios[previous_ratio_index] * r ... ratios.append(ratio) ... >>> ratios [0.004999999999999999, 0.0045, 0.00405, 0.003645, 0.0032805, 0.00295245, 0.002657205, 0.0023914845000000003, 0.00215233605, 0.0019371024450000002, 0.0017433922005000001, 0.00156905298045, 0.001412147682405, 0.0012709329141645, 0.00114383962274805, 0.001029455660473245, 0.0009265100944259205, 0.0008338590849833285, 0.0007504731764849957, 0.0006754258588364961, 0.0006078832729528464] >>> sum(ratios) 0.04452905054342437
Regarding to the fulfilness criteria, the maximum number of items stored in given filter for fill ratio 50% is given by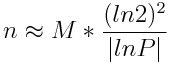 
Where M is total number of bits and P the false positive probability. From that the number of slices is computed with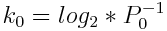 
. The number of slices for new filters is computed with the tightening ratio as 
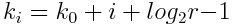. Px represents error probability for xth created filter and r is tightening ratio such as 0 < r < 1.
Since Scalable Bloom filter uses the variant with bit vector size divided on k slices, the number of hash functions automatically corresponds to the number of slices (since each functions works on its own slice).
Examples
The examples below use python-bloomfilter library providing an implementation for Scalable Bloom filter:
import unittest
from pybloom.pybloom import ScalableBloomFilter
class ScalableBloomFilterTest(unittest.TestCase):
def should_keep_the_false_positives_small_after_resizing_11_times(self):
scalable_bloom_filter = ScalableBloomFilter(mode=ScalableBloomFilter.SMALL_SET_GROWTH)
count = 150000
for i in range(0, count):
scalable_bloom_filter.add(i)
for number in range(0, count):
# Checks for false negatives
is_in_set = number in scalable_bloom_filter
self.assertTrue(is_in_set, "Number {nr} should be in the filter".format(nr=number))
self.assertEqual(11, len(scalable_bloom_filter.filters))
false_positives = 0
out_of_range_max = count*2
for number in range(count, out_of_range_max):
contains_out_range = number in scalable_bloom_filter
if contains_out_range:
false_positives += 1
# We got ~ 0.02% of false positives, a little bit worse than the error rate of 0.001
false_positives_percentage = float(false_positives)*100.0/float(out_of_range_max)
self.assertEqual(false_positives_percentage, 0.0276666666667)
def should_resize_the_filter_after_reaching_the_threshold_twice(self):
scalable_bloom_filter = ScalableBloomFilter(initial_capacity=50, error_rate=0.05,
mode=ScalableBloomFilter.SMALL_SET_GROWTH)
for number in range(0, 100):
scalable_bloom_filter.add(number)
self.assertEqual(2, len(scalable_bloom_filter.filters), "The filter should be resized twice")
def should_show_decreasing_error_rate(self):
max_range = 1500000
scalable_bloom_filter = ScalableBloomFilter(initial_capacity=100000, error_rate=0.1,
mode=ScalableBloomFilter.SMALL_SET_GROWTH)
for number in range(0, max_range):
scalable_bloom_filter.add(number)
expected_rates = [0.009999999999999998, 0.009, 0.0081, 0.00729]
index = 0
for filter in scalable_bloom_filter.filters:
self.assertEqual(filter.error_rate, expected_rates[index])
index += 1
Scalable Bloom filter is one variety of Bloom filter. It addresses the problem of unbounded data and thanks to it we don't need to know the size of dataset before constructing the filter. Scalable Bloom filter adapts to the execution and increasing number of elements by creating new basic filters able to store expotentially more items than previous ones. They're created once a fulfilness threshold is reached. However the growth is infinite and this kind of filters work well without memory constraints.
