Bloom filter

Versions: Algerbird 0.13.4

After HyperLogLog and Count-min sketch it's time to cover another popular probabilistic algorithm - Bloom filter.

Bloom filter is explained in 3 parts. Th first defines the algorithm and also shows its use cases. The second one talks briefly about false positives while the last shows Bloom filter in action throughout Algerbird's implementation. This post is the first from the series about Bloom filters. Further posts will present subtypes of the algorithm described here.

Definition

Bloom filter is another space-efficient probabilistic data structure letting us to check if given element is in the set. Thanks to that it can be used for instance to detect duplicates or to avoid to make unnecessary I/O operations in some databases (membership is verified before reading the data physically).

The algorithm is based on a bit vector of size m and k independent and uniformly distributed hash functions. When a new element is handled by the filter, it's hashed against each of the functions. Their results correspond to the bit vector indexes that will be set to 1. The same operation is made to check membership. The algorithm reads the values from the computed indexes and depending on the result, it tells whether:

• the element is certainly not in the set - if one of received values is equal to 0
• the element is probably in the set - if all received values are equal to 1

The following image summarizes the logic behind Bloom filter:

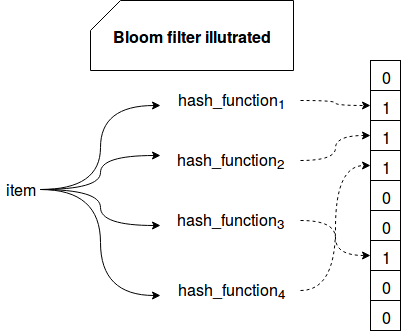
Hence the false positive matches are possible, i.e. we can certainly exclude an element from the set but we can only probably tell that it's in the set. In the other side, Bloom filter never returns false negatives (at least in its basic version, it's possible in other subtypes as Stable Bloom filter covered in one of next posts).

The efficiency of Bloom filter relies on the size of the bit vector. The precision decreases as soon as the vector fulfills since every value will be returned as present (no more space with 0). Thus it's not a good solution for unbounded data. Moreover, the basic version of Bloom filter doesn't support removals and it can only grow up. Fortunately this basic version was extended in a lot of fields. Scalable Bloom filter supports removals, Stable Bloom filter fits to unbounded (e.g. streaming) data and Layered Bloom filter helps to track the number of times when given item was added to the set.

In our daily work we can meet Bloom filter in Apache Cassandra where it's used to verify if the requested data may exist in one of SSTables. Since Bloom filter is able to exclude the presence of given element in the dataset, it avoids unnecessary lookups and I/O operations.

False positives

Two formulas are important to reduce false positives. The first one defines the false positives rate:

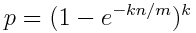
m represents the size of the bit vector, n represents the number of inserted keys and k is the number of hash functions. Since the size of the bit vector depends on the expected number of elements, we can set k as:

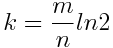
The number of hash functions should be a trade-off between the accuracy and the performance. If we have too few hash functions, the risk of receiving false positives increases. In the other side we risk to slow down the response time.

Bloom filter examples

Bloom filter is one of approximate data types provided in Algerbird. It's used in the following snippets to show how Bloom filter works:

behavior of "Bloom filter"

it should "return a lot of false positives with too few hash functions" in {
  val hashFunctions = 1
  val bitVectorSize = 200
  val bfMonoid = new BloomFilterMonoid[Int](hashFunctions, bitVectorSize)

  val bloomFilter = bfMonoid.create((1 to 100): _*)

  val contains1 = bloomFilter.contains(1)
  contains1.isTrue shouldBe true
  // As you can see, despite the size of bit vector we can still retrieve false positives
  // because of too few hash functions
  val firstNotMatching = (101 to 200).find(nr => bloomFilter.contains(nr).isTrue)
  firstNotMatching.get shouldEqual 103
}

it should "not generate false positives with optimal width and number of hash functions" in {
  val nrOfItems = 1400
  val falsePositiveRatio = 0.05
  val optimalWidth = BloomFilter.optimalWidth(nrOfItems, falsePositiveRatio)
  val hashFunctions = BloomFilter.optimalNumHashes(nrOfItems, optimalWidth.get)
  val bfMonoid = new BloomFilterMonoid[Int](hashFunctions, optimalWidth.get)

  val bloomFilter = bfMonoid.create((1 to nrOfItems): _*)

  // As told Bloom filter definitively exclude some items from the set
  (nrOfItems+1 to 600).foreach(nr => {
    val containsResult = bloomFilter.contains(nr)
    containsResult.isTrue shouldBe false
  })
  // Here we check the items not in the set that should be in it - thanks to optimal width and
  // number of hash functions, we don't get them
  val itemsNotInSet = (1 to nrOfItems).filter(nr => !(bloomFilter.contains(nr).isTrue))
  itemsNotInSet shouldBe empty
  // We can safely evaluate the membership of 1400 items with 5 hash functions and a bit vector of 8730 length
  hashFunctions shouldEqual 5
  optimalWidth.get shouldEqual 8730
}

it should "return a lot of false positives because of too small bit vector" in {
  // We use similar configuration to the one from the previous test except the size of bit vector that was reduced from
  // 8730 to 1000
  val bitVectorSize = 1000
  val entriesNumber = 1400
  val hashFunctions = 5
  val bfMonoid = new BloomFilterMonoid[Int](hashFunctions, bitVectorSize)

  val bloomFilter = bfMonoid.create((1 to entriesNumber): _*)

  // Check how many items are incorrectly classified as maybe in the dataset
  val incorrectlyInSet = (entriesNumber+1 to entriesNumber+600).filter(nr => bloomFilter.contains(nr).isTrue)
  incorrectlyInSet should have size 591
  val itemsNotInSet = (1 to entriesNumber).filter(nr => !(bloomFilter.contains(nr).isTrue))
  itemsNotInSet shouldBe empty
}

This post shown some points about Bloom filters. Based on similar principles than previously described Count-min sketch and HyperLogLog, it uses hash functions and a bit vector to test the membership of an element in given dataset. It's space efficient and with optimal settings lets to highly reduce false positive rate. However, it's unable to tell that tested element belongs certainly to the dataset. Instead it can only tell that it certainly doesn't belong to the dataset. Another drawback is the lack of adaptation for unbounded datasets by the basic version of Bloom filter. Fortunately some extensions exist and can be used to deal with such kind of data.