This post follows the series about approximation algorithms. But unlike before, this time we'll focus on simpler solution, the linear probabilistic counting.
The post is organized in 2 sections. The first one describes the fundamentals of the solution. The second one gives its example of implementation in AddThis streamlib library.
Linear probabilistic counting explained
Linear probabilistic counting is used to estimate the cardinality of given dataset. Thus it answers the question about the number of unique items within it. An example of its use could be the counter of unique visitors in a website. This problem could be solved with a solution based on hash sets however in terms of storage it's less efficient that the algorithm described here. The hash set-based solution will obviously store the items while it's not a requirement needed to estimate the cardinality.
In the other side, linear probabilistic counting is based on the similar concept than the basic solution (hashing) but it doesn't require to store the objects themselves. A single bit is enough to determine if given element was already seen or not. First the algorithm initializes a bit map where all entries are set to 0. Now every time when new event is processed, it's firstly hashed to the number representing a key of the bit map. The value corresponding to this index is later changed to 1. The cardinality estimation is later a result of:
-m * ln V where: m - the size of the bit map V - the ratio of empty entries (value set to 0) on the size of the bit map (empty_nr/m)
As you can deduce, in this solution we need to know the size of the map before the execution. And since it has an impact on the estimation error, it's a pretty important parameter. If the map is too small compared to the data size, then the risk of hash collisions is bigger. In the other side, when the map is too big, then the risk of collisions is much smaller but the solution wastes the space. It's then important to find the size of the map letting us to keep the estimation error low. Two factors have an influence on the map size:
- standard error - defines how different will be the estimation from the real results
- fill-up proability - defines the probability of the map becoming full (= number of dataset elements >= map size). It obviously happens when the n/m (expected cardinality / map size) > 1
To determine the map size the article explaining linear probabilistic counting, "A Linear-Time Probabilistic Counting Algorithm for Database Applications", provides a table where it defines map sizes respecting 1% of standard error below 0.7% of map saturation for given dataset maximum expected cardinality. Another method returning the map size consists on the binary search where m must respect the specified standard error:
standard_error = (√m (et - t - 1)1/2) / n where n - the maximum expected cardinality of the dataset t - n/m
The whole logic of linear probabilistic counting can be summarized in the following schema:
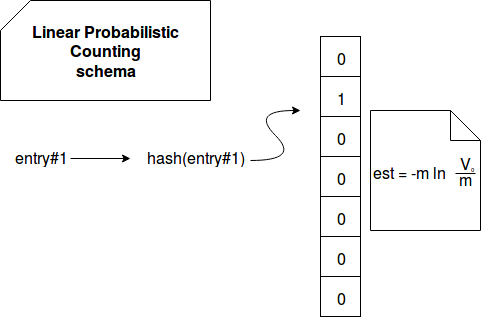
Despite of the simplicity, linear probabilistic counting suffers from some of drawbacks. The main visible one is the required knowledge of the dataset maximum cardinality that directly impacts the size of the map. For some use cases it may be difficult to estimate.
Linear probabilistic counting example
As already told to show an example of the linear probabilistic counting we'll see the efficiency of AddThis implementation:
behavior of "linear probabilistic counting"
it should "give accurate results when the map is correctly sized" in {
val accurateLinearCounting = LinearCounting.Builder.withError(0.05d, 100).build()
val data = (0 until 100)
data.foreach(entry => accurateLinearCounting.offer(entry))
accurateLinearCounting.cardinality() shouldEqual 100
}
it should "give less accurate results when the map is too small" in {
val inaccurateLinearCounting = LinearCounting.Builder.withError(0.05d, 10).build()
val data = (0 until 1000)
data.foreach(entry => inaccurateLinearCounting.offer(entry))
// Because of too small map size, the error ratio is here bigger
// but still less than 5% (3.4%)
inaccurateLinearCounting.cardinality() shouldEqual 966
inaccurateLinearCounting.isSaturated shouldBe false
}
it should "give completely inaccurate result when the map is too small" in {
val inaccurateLinearCounting = LinearCounting.Builder.withError(0.05d, 10).build()
// Instead of 1000 we deal with 10000-items dataset
val data = (0 until 10000)
data.foreach(entry => inaccurateLinearCounting.offer(entry))
// Here the counter is saturated, i.e. it's really to small to handle
// the results correctly
inaccurateLinearCounting.cardinality() shouldEqual Long.MaxValue
inaccurateLinearCounting.isSaturated shouldBe true
}
This another post about approximation algorithms presented a simpler alternative for HyperLogLog explained previously. It's called linear probabilistic counting and it's also based on the hashing principle. However, it uses a single bit map. This simplicity is on the same time a limitation of the algorithm since we need to know pretty exactly the size of the dataset before creating the map. And in some specific cases this information can be difficult to gather.
