Counting the number of distinct elements can appear a simple task in classical web service-based applications. After all, we usually have to deal with a small subset of data that simply fits in memory and can be automatically counted with the data structures as sets. But the same task is less obvious in Big Data applications where the approximation algorithms can come to the aid.
Data Engineering Design Patterns

Looking for a book that defines and solves most common data engineering problems? I wrote
one on that topic! You can read it online
on the O'Reilly platform,
or get a print copy on Amazon.
I also help solve your data engineering problems 👉 contact@waitingforcode.com 📩
HyperLogLog is one of approximation algorithms that can be used to resolve counting problem and this post covers it. The first section explains the main ideas of the HyperLogLog. The second explains the role of registers. The last part contains some tests that reveal when HyperLogLog performs well and when it works worse.
HyperLogLog ideas
HyperLogLog is an approximation algorithm, so it doesn't provide exact results. However, the margin of error is about 2% that in the case of a big dataset can often be an acceptable trade-off between the accuracy and performance. The general idea of the algorithm consists on counting the number of leading 0 in object's hash binary representation. To understand it better, let's zoom a little on the steps made by HyperLogLog:
- each counted entry is transformed to the binary representation by a hash function common to all entries
The hash function comes with some obligations. First of all, for two equal values it has to generate the same hashes. Secondly, each bit of hashed value must have the same probability of being 0 or 1 (1⁄2) - binary representation is analyzed - the algorithm searches the leftmost 1 bit. For instance, if the representations begins with 1, then the number is 1. In the other side, when the representation starts with 000001, then the number is 6.
This method of analysis is called bit-pattern observable. It consists on checking certain number of bits occurring at the beginning of the binary values.
HyperLogLog counts the number of 0 in order to search the bit patterns that have low possibility to occur. The pattern with a lot of 0 is considered as a big number, so a large dataset. It's based on assumption that the approximate cardinality of so number is about 2^$pattern_size (but this approach is very approximate and it's why the next steps are done) - so counted number of leading 0 (let's call it nnow) is later compared with the previously seen number of leading 0 (nprevious). If nnow is greater than nprevious, it becomes new nprevious.
- at the end the dataset cardinality is estimated (E) with the following formula:
E = αm * m2 * Z
where αm is a constant correcting a systematic multiplicative bias, m is the number of registers and Z is the geometric mean of registers: m∑j=1 2-M[j]
The above points can be resumed in the following image:
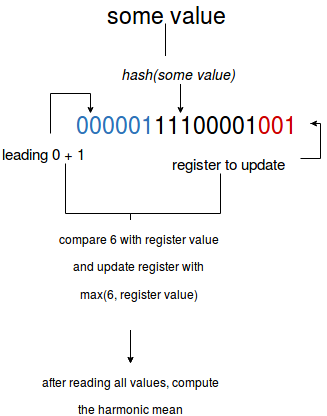
Registers
It's important to notice that the max numbers of leading 0 are stored in the structures called registers (other name in use is bucket). The number of registers is computed from the number of bits used to retrieve register's index from the binary representation. If we take b as this number of bits, then the number of registers to create is computed as 2b. For instance, if the index is represented by first 3 bits, then 2*2*2 (8) registers are created.
The role of registers is important. They determine the approximation error of HyperLogLog with this formula: 1.03896/√numberOfRegisters. As you can deduce more registers guarantee better accuracy. Nevertheless greater number of indexes increases the amount of memory required to approximate the cardinality (even though this amount will be still smaller as if we'd use the naive method of counting, for instance the one using set data structure).
The registers are also related to another point - hashing function. As already told, a good hashing function must guarantee even distribution among registers. It leads to the situation when each register handles up to numberOfAllElements/numberOfRegisters elements. In other case (= uneven distribution) it can lead to the presence of a large variance (outliers). A method employed by HyperLogLog to decrease this effect is the merge of values stored by registers with harmonic mean instead of geometric mean used by LogLog (HyperLogLog is an evolution of LogLog).
HyperLogLog tests
In order to demonstrate HyperLogLog features we'll use its version from Twitter's Algerbird library. The goal in this section is to check the approximation accuracy and the parameters influencing the results:
"hll with more bits" should "have better accuracy" in {
val upperBound = 500000
val itemsToTest = (1 to upperBound)
val hllMonoid4Bits = new HyperLogLogMonoid(bits = 4)
val hllMonoid8Bits = new HyperLogLogMonoid(bits = 8)
val hllMonoid16Bits = new HyperLogLogMonoid(bits = 16)
val hllMonoid20Bits = new HyperLogLogMonoid(bits = 20)
val hlls4BitsEstimate = hllMonoid4Bits.sum(itemsToTest.map(nr => hllMonoid4Bits.create(int2Bytes(nr))))
val hlls8BitsEstimate = hllMonoid8Bits.sum(itemsToTest.map(nr => hllMonoid8Bits.create(int2Bytes(nr))))
val hlls16BitsEstimate = hllMonoid16Bits.sum(itemsToTest.map(nr => hllMonoid16Bits.create(int2Bytes(nr))))
val hlls20BitsEstimate = hllMonoid20Bits.sum(itemsToTest.map(nr => hllMonoid20Bits.create(int2Bytes(nr))))
// As you can see through the measurements below, more bits are allocated to registers
// (= thus more registers are created), more accurate the results are
// It's shown in the comment:
// https://github.com/twitter/algebird/blob/develop/algebird-core/src/main/scala/com/twitter/algebird/HyperLogLog.scala#L231
hlls4BitsEstimate.approximateSize.estimate shouldEqual 474165
hlls8BitsEstimate.approximateSize.estimate shouldEqual 486507
hlls16BitsEstimate.approximateSize.estimate shouldEqual 498975
hlls20BitsEstimate.approximateSize.estimate shouldEqual 499498
}
"the estimate for small quantity of data" should "be low because of too few bits used in registers" in {
val upperBound = 5
val itemsToTest = (1 to upperBound) ++ (1 to upperBound) ++ (1 to upperBound) ++ (1 to upperBound/2)
val hllMonoid4Bits = new HyperLogLogMonoid(bits = 4)
val hlls4BitsEstimate = hllMonoid4Bits.sum(itemsToTest.map(nr => hllMonoid4Bits.create(int2Bytes(nr))))
hlls4BitsEstimate.approximateSize.estimate shouldEqual 4
}
"hll accuracy" should "be kept for 20 bits indexes even with a lot of duplicates" in {
val upperBound = 500000
val itemsToTest = (1 to upperBound) ++ (1 to upperBound) ++ (1 to upperBound) ++ (1 to upperBound/2)
val hllMonoid20Bits = new HyperLogLogMonoid(bits = 20)
val hlls20BitsEstimate = hllMonoid20Bits.sum(itemsToTest.map(nr => hllMonoid20Bits.create(int2Bytes(nr))))
// The accuracy for 20-bits index is still the same - even if we encounter more than 3 times duplicated items
hlls20BitsEstimate.approximateSize.estimate shouldEqual 499498
}
"hll" should "be created from acceptable approximation error" in {
val upperBound = 500000
val itemsToTest = (1 to upperBound)
val agg = HyperLogLogAggregator.withErrorGeneric[Int](0.0001)
val combinedHll: HLL = agg(itemsToTest)
// As you can see, here the results are even more accurate than in the previous cases
// It's because under-the-hood the HyperLogLogAggregator converts the acceptable error rate
// to a number of bits used by registers (27 instead of 20 bits from previous example)
combinedHll.approximateSize.estimate shouldEqual 499947
}
Counting distinct elements in Big Data applications having millions of entries can be a difficult task. Every naive method requires a lot of memory. Fortunately sometimes approximation results can be used and they're pretty well provided by HyperLogLog algorithm. It's based on the idea of bit-pattern observables and harmonic mean applied on the longest runs of 0-bits + 1 stored in independent registers. As shown in the last section, the number of the registers but also the number of analyzed values have an important influence on the accuracy.
Consulting

With nearly 17 years of experience, including 9 as data engineer, I offer expert consulting to design and optimize scalable data solutions.
As an O’Reilly author, Data+AI Summit speaker, and blogger, I bring cutting-edge insights to modernize infrastructure, build robust pipelines, and
drive data-driven decision-making. Let's transform your data challenges into opportunities—reach out to elevate your data engineering game today!
👉 contact@waitingforcode.com
🔗 past projects


