Even though Bloom filter perfectly suits to bounded data it also has some interesting implementations for unbounded sources too. One of them is Stable Bloom filter.
In this post we'll try to see how Stable Bloom filter can be used to deal with unbounded data and still keep quite low false positives ratio. Its first section explains the basic ideas behind this algorithm. The second part covers the risk of false negatives while the third one focuses on the parameters impacting the final results. In the final part we'll see an use of Stable Bloom filter throughout one of Open Source implementations.
Definition
As already explained in the post about Scalable Bloom filter basic Bloom filter doesn't work with unbounded data source. The number of "free" 0 in the hash table decreases with time and thus, after some period, all entries are detected as "may be in the set". Scalable Bloom filter described in another previous post addresses this issue by creating new filters after filling current one at some ratio. Stable Bloom filter takes another approach since it transforms the 0/1 bit to incrementable and decrementable counters.
The bits vector is hence transformed to a vector of counters where the min value is 0 and the max is computed from 2d - 1 where d represents the number of bits allocated in each vector's cell. Checked item is still hashed by k uniform and independent hash functions. The difference starts when their results interact with the vector. When the data is added, some of P randomly chosen indexes are decremented by 1. After that the indexes computed by hash functions are set to the max value. During the reading, if at least one of values from hashed fields is equal to 0, the filter considers that the item already exists in the set. The whole process is summarized in the following schema:
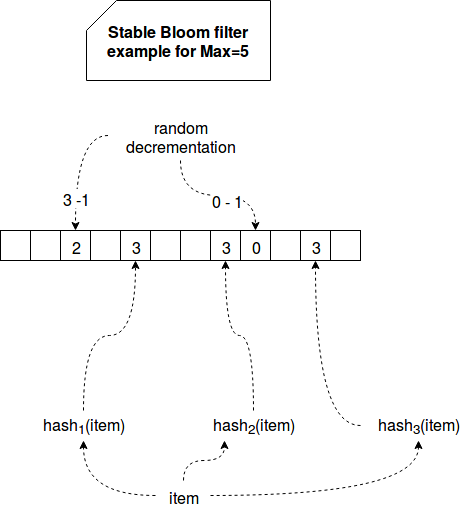
Stable Bloom filter is characterized by 2 stability characteristics. First of them is stable property. The false positives ratio depends on the faction of zeros in the filter. As proven in Approximately Detecting Duplicates for Streaming Data using Stable Bloom Filters paper, these fractions become fixed after some number of iterations, independently on the setup parameters and under the condition that the size of input stream (N) is large enough. The expected fraction of 0s converges at exponential rate. Stable property brings in its own the stable point. It's defined as a threshold of expected fractions of 0s when the number of iterations goes to infinity. Stable Bloom filter is considered as stable once this limit reached.
False negatives
Unlike Bloom filter, Stable Bloom filter introduces the risk of false negatives, i.e. situation where duplicated elements are wrongly detected as distinct. It a duplicated element called xi arrives once again to the filter it has a risk to be detected as unique. The risk comes from the fact that one of its hasging indexes could be randomly set to 0 during y iterations from the moment it was seen for the first time. Obviousy, when the element is seen for the first time (= it doesn't have predecessors), the risk for false negative results is 0.
Parameters
Correctly set parameters help to reduce the risk of false negatives and a whole efficiency of the filter. Three settings are important in Stable Bloom filter. The first one is called P and represents the number of randomly picked cells decremented by 1 at each iteration. It's computed with the following formula:
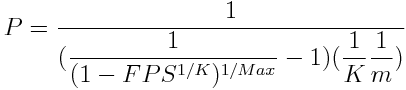
Where m is the number of cells in the filter, K the number of hash functions, Max the value a cell is set to and FPS the acceptable false positives ration. From that we can tell that P depends on K, FPS and Max and not on m since K is often much larger than m.
Regarding to the second parameter, the number of hash functions K, it can minimize the false negatives ratio. It depends on already covered FPS and Max parameters. It means that K doesn't depend on the input stream and the amount of space m. As proven in the scientific article introducing the filter, we can chose optimal value of K from false negative rates computed from K that in its turn is based on FPS and Max. For instance, for Max=3 and FPS=0.01, the optimal number of K will be between 4 and 5. For Max=1 and FPS=0.01, K will be 2. More details are given in the paper.
The third important property is the value a cell is set to called Max. Unlike K it depends on the input size. Max helps to reduce the number of false negatives. It uses space effectively when it's set to 2d - 1 where d is the number of bits allocated per cell. It's important to keep in mind the impact of Max on P, i.e. on time cost. Larger Max is, more random cells need to be set to 0. For instance, for Max=1, FPS=0.01 and K=3, the number of such cells will be 10 but for Max=15, FPS=0.01 and K=6 it will be already 141. According to the paper, a practical choice for Max will be 1, 3 or 7. It can be larger though if a higher time cost is tolerated.
Examples
Let's see now how Stable Bloom filter parameters behave in one of available implementations (). Some class fields were modified to make them public and see the impact of different parameters on the efficiency of the filter:
behavior of "Stable Bloom filter"
// Please note StableBloomFilter private and final fields were made public to simplify testing
it should "not find false positives with low false positives rate" in {
val m = 1000000
val stableBloomFilter = StableBloomFilter.builder()
.withBitsPerBucket(8)
.withExpectedNumberOfItems(m)
.withFalsePositiveRate(0.01d).build()
val data = (0 to 100000).map(nr => s"${nr}").toSet.asJava
stableBloomFilter.put(data)
val falseNegatives = data.asScala.filter(numberInSet=> !stableBloomFilter.mightContain(numberInSet))
falseNegatives shouldBe empty
val falsePositives = (100001 to 100000*5).map(nr => nr.toString)
.filter(nrAsString => stableBloomFilter.mightContain(nrAsString))
falsePositives shouldBe empty
stableBloomFilter.bitsPerBucket shouldEqual 8
stableBloomFilter.numHashFunctions shouldEqual 7
stableBloomFilter.numOfBuckets shouldEqual 9585058
// Exactly as defined in the article, larger Max (here bitsPerBucket), more buckets must be decremented each time
stableBloomFilter.bucketsToDecrement shouldEqual 2442
}
it should "have more false positives with higher false positives rate" in {
// As above but we increase accepted false positives rate
// Logically the number of false positives will increase
val m = 1000000
val stableBloomFilter = StableBloomFilter.builder()
.withBitsPerBucket(8)
.withExpectedNumberOfItems(m)
.withFalsePositiveRate(0.1d).build()
val data = (0 to 100000).map(nr => s"${nr}").toSet.asJava
stableBloomFilter.put(data)
val falseNegatives = data.asScala.filter(numberInSet=> !stableBloomFilter.mightContain(numberInSet))
falseNegatives shouldBe empty
val falsePositives = (100001 to 100000*5).map(nr => nr.toString)
.filter(nrAsString => stableBloomFilter.mightContain(nrAsString))
falsePositives should have size 104
stableBloomFilter.bitsPerBucket shouldEqual 8
// The false negatives come from smaller number of hash functions and number of buckets
stableBloomFilter.numHashFunctions shouldEqual 3
stableBloomFilter.numOfBuckets shouldEqual 4792529
// Here since the number of hash functions is smaller than in above test, the number of decremented
// buckets is also smaller. However it doesn't have a positive impact on the data
// Even though the rate of false negatives remain quite low (0.02%)
stableBloomFilter.bucketsToDecrement shouldEqual 1224
}
it should "keep slightly the same number of false negatives even if the number of bits per bucket is smaller" in {
val m = 1000000
val stableBloomFilter = StableBloomFilter.builder()
.withBitsPerBucket(3)
.withExpectedNumberOfItems(m)
.withFalsePositiveRate(0.1d).build()
val data = (0 to 100000).map(nr => s"${nr}").toSet.asJava
stableBloomFilter.put(data)
// Smaller number of bits made first false negatives appear
val falseNegatives = data.asScala.filter(numberInSet=> !stableBloomFilter.mightContain(numberInSet))
falseNegatives should have size 1
val falsePositives = (100001 to 100000*5).map(nr => nr.toString)
.filter(nrAsString => stableBloomFilter.mightContain(nrAsString))
falsePositives should have size 104
stableBloomFilter.bitsPerBucket shouldEqual 3
// The number of false negatives is the same as above. But unlike the previous case, here we use only 3 bits per
// bucket
stableBloomFilter.numHashFunctions shouldEqual 3
stableBloomFilter.numOfBuckets shouldEqual 4792529
// The number of decremented buckets decreased 4 times
stableBloomFilter.bucketsToDecrement shouldEqual 32
}
it should "increase the number o false negatives and false positives because of smaller size of filter" in {
val m = 10000
val stableBloomFilter = StableBloomFilter.builder()
.withBitsPerBucket(3)
.withExpectedNumberOfItems(m)
.withFalsePositiveRate(0.1d).build()
val data = (0 to 100000).map(nr => s"${nr}").toSet.asJava
stableBloomFilter.put(data)
val falseNegatives = data.asScala.filter(numberInSet=> !stableBloomFilter.mightContain(numberInSet))
(falseNegatives.size > 82511 && falseNegatives.size < 82764) shouldBe true
val falsePositives = (100001 to 100000*5).map(nr => nr.toString)
.filter(nrAsString => stableBloomFilter.mightContain(nrAsString))
(falsePositives.size > 40200 && falsePositives.size < 40500) shouldBe true
}
This post presented the main points of Stable Bloom filter. As we could learn it's adapted to dealing with unbounded data thanks to the system of "counters" in filter vector. Each time when new item is handled, the indexes computed from hash functions are set to a maximal value (usually 3, 5, 7). But before that some randomly chosen cells are also decremented by 1 in order to avoid the situation where the filter is saturated. However, Stable Bloom filter has also some drawbacks and one of them is the introduction of false negatives that, as we could see in the 3rd part tests, may happen if the filter and the number of bits per bucket are too small.
