Previous post about the Conflict-free Replicated Data Types presented some of basic structures of this type. This one will describe some of recently uncovered types such as: flags, graphs and arrays.
Data Engineering Design Patterns
Looking for a book that defines and solves most common data engineering problems? I'm currently writing
one on that topic and the first chapters are already available in π
Early Release on the O'Reilly platform
I also help solve your data engineering problems π contact@waitingforcode.com π©
The post is divided in 4 sections. The first one describes the flags in the context of CRDT. The next one is about the graphs that can also benefit from CRDT convergence properties. The final part describes the maps. Each of the sections contains some code examples for described data type.
CRDT: flags
Before talking about the CRDT and flags, let's begin by describing the flags shortly. The flag is a data structure holding a boolean value. The value represents disabled or enabled state. In the context of CRDT, the flags are not commutative since (enable, disable) and (disable, enable) doesn't mean the same.
Because of the not-commutative character we distinguish 2 types of flags:
- Enable-Wins Flag - two concurrent disable and enable always leave the flag in enable state.
- Disable-Wins Flag - it's the opposite of the above, the disable flag is always left when 2 concurrent writes happen.
Illustrating the flags is quite straightforward:
class FlagCrdtTest extends FlatSpec with Matchers {
"flag" should "be always merged to true" in {
val trueFlagNode1 = Flag.empty.switchOn
val falseFlagNode2 = Flag.empty
val mergedFlag = falseFlagNode2.merge(trueFlagNode1)
mergedFlag.enabled shouldEqual true
}
}
CRDT: graphs
The use of the CRDT can also be retrieved in the graphs. As a reminder, the graph is composed of vertice - edge pairs. This relationship makes that the operations on vertices and edges can't be independent: an edge can be added only if the corresponding vertex exists and a vertex can be removed only if it doesn't have any edges. When these 2 operations are called concurrently, 3 scenarios are expected:
- Giving a precedence for removals - all edges are removed as a side effect
- Giving a precedence for adds
- Delaying the execution of removal after the execution of all add operations (drawback: synchronization is expected)
To deal with these problems easier, the CRDT proposes 3 graph-like data structures:
- Add-only monotonic Directed Acyclic Graph - this first type of the graph is a DAG, thus a graph without cycles and with directed edge between vertices. It's initialized with 2 sentinels marking the beginning and the end of the graph and can be illustrated with these two points:
- a new edge can be added only if it follows the same direction as the already existent path. This property prevents the graph against becoming cyclic.
- the monotonicity is about the add operations that can concern the same element (vertices or edges) or different ones. For the first case, if the adds on the same element are executed concurrently, the executions always generate the same results (idempotency). For the latter case the manipulated objects are different, so there is no impact of concurrent write.
Such graph has 2 writing operations: addBetween and addEdge. The former one adds an vertex between 2 vertices. The latter one adds new edge between 2 vertices. However, this data structure is not perfect to deal with removals (hence add-only). The removal is problematic since, if it concerns 2 different vertices but linked directly, the merge may not be possible to do, as in the following image: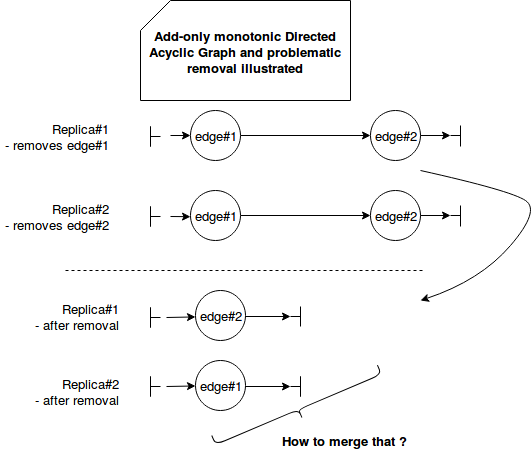
- Add-Remove Partial Order data type - the solution to the removal problem is the Add-Remove Partial Order data type. Here the graph is represented as a DAG where removed vertices are retained as tombstones (= they still exist but are not read). Thanks to that, even if a concurrent remove/add operation is executed, the result will remain consistent.
- 2P2P-Graph - as the name indicates, it combines 4 2P-Sets where one represents graph vertices (adds + removals) and other one the graph edges (adds + removals). The use of 2P-Sets implies the removal-wins semantic in the case of concurrent add edge and remove vertex operations. The removals are always executed in the last position (after add). So we tell that the removal takes the precedence over the add. As told, the side-effect of this strategy is the automatic removal of all edged for given vertex.
- Replicated Growable Array (RGA) - the graph is represented as a linked list of vertices where the vertex in this graph are enriched with the timestamp property. The timestamp must be positive, unique and must increase with causality (= at every new event; if t happens before t', the timestamp t' > t). The timestamp is generated at the moment of adding new element, locally at replica level.
The graph supports insert and removal operations. For the former one it happens throughout the method called addRight(v, a) where new vertice is added to the right of the first vertice (v). If 2 operations occur concurrently and concern the same element (e.g. addRight(v, a); addRight(v, b)), the operation with greater timestamp wins, i.e. it's appended to the left of the earlier operation (= (v) -> (b) -> (a)).
The removal operation doesn't delete the vertices but instead it marks them as tombstones. This solution prevents against the problem of concurrent add and remove methods since the removed vertice is not physically deleted from the graph and even in the case of concurrent manipulations, the result can be merged. Thanks to that property coming from Add - Remove Partial Order, the RGA is considered as a CRDT type.
The graphs are not present in Akka Distributed Data. It's why we'll focus here on a simple implementation for RGA and 2P2P-Graph:
/**
* CRDT graph tests. The implementation code was inspired from the specifications defined in
* "A comprehensive study of Convergent and Commutative Replicated Data Types"
* that can be found here https://hal.inria.fr/file/index/docid/555588/filename/techreport.pdf
*/
class GraphsCrdtTest extends FlatSpec with Matchers {
"RGA" should "create correct graph even if the events arrive in disorder" in {
val rga = new ReplicatedGrowableArray()
rga.addRight(RgaId("sentinel_left", -1L), RgaId("A", 1L))
rga.addRight(RgaId("A", 1L), RgaId("C", 3L))
rga.addRight(RgaId("A", 1L), RgaId("B", 2L))
val mappedRga = rga.getGraph.map(rgaId => rgaId.id)
mappedRga shouldEqual Seq("sentinel_left", "A", "C", "B", "sentinel_right")
}
"RGA" should "create correct graph if the events arrive in order" in {
val rga = new ReplicatedGrowableArray()
rga.addRight(RgaId("sentinel_left", -1L), RgaId("A", 1L))
rga.addRight(RgaId("A", 1L), RgaId("B", 2L))
rga.addRight(RgaId("A", 1L), RgaId("C", 3L))
val mappedRga = rga.getGraph.map(rgaId => rgaId.id)
mappedRga shouldEqual Seq("sentinel_left", "A", "C", "B", "sentinel_right")
}
"the 2P2P Graph" should "only mark elements as removed and keep them in the map" in {
val graph2P2P = new TwoPhaseTwoPhaseGraph
graph2P2P.addVertex("A")
graph2P2P.addVertex("B")
graph2P2P.addVertex("C")
graph2P2P.addEdge("A", "B")
graph2P2P.addEdge("B", "C")
graph2P2P.removeEdge("A", "B")
val graphEdges = graph2P2P.getEdges
graphEdges should have size 1
graphEdges should contain only(("B", "C"))
graph2P2P.getAddedEdges should have size 2
graph2P2P.getAddedEdges should contain allOf(("A", "B"), ("B", "C"))
graph2P2P.getRemovedEdges should have size 1
graph2P2P.getRemovedEdges should contain only(("A", "B"))
}
}
class TwoPhaseTwoPhaseGraph {
// Normally we'd use a 2PSet instead of Set but it doesn't exist in the Akka Distributed Data
// and since the code is only for illustration purposes, it's easier to use a simple Set
private val verticesAdded = mutable.Set[String]()
private val verticesRemoved = mutable.Set[String]()
private val edgesAdded = mutable.Set[(String, String)]()
private val edgesRemoved = mutable.Set[(String, String)]()
def getEdges: mutable.Set[(String, String)] = {
edgesAdded.filter(edge => !edgesRemoved.contains(edge))
}
def getAddedEdges: mutable.Set[(String, String)] = edgesAdded
def getRemovedEdges: mutable.Set[(String, String)] = edgesRemoved
def addVertex(vertex: String) = verticesAdded.add(vertex)
def addEdge(vertexSource: String, vertexTarget: String): Unit = {
assert(checkIfVertexExists(vertexSource), "Source vertex must exist in the graph")
assert(checkIfVertexExists(vertexTarget), "Target vertex must exist in the graph")
edgesAdded.add((vertexSource, vertexTarget))
}
private def checkIfVertexExists(vertex: String): Boolean = {
verticesAdded.contains(vertex) && !verticesRemoved.contains(vertex)
}
def removeEdge(vertexSource: String, vertexTarget: String): Unit = {
val edgeToRemove = (vertexSource, vertexTarget)
assert(edgesAdded.contains(edgeToRemove), "The removed edge must exist")
edgesRemoved.add(edgeToRemove)
}
}
class ReplicatedGrowableArray {
private val graph = mutable.ListBuffer[RgaId]()
graph.append(RgaId("sentinel_left", -1L))
graph.append(RgaId("sentinel_right", 0L))
def getGraph: mutable.ListBuffer[RgaId] = graph
def addRight(sourceVertex: RgaId, newVertex: RgaId): Unit = {
// As it's only for illustration purposes, it's simplified version where no downstream operation
// is propagated, i.e. we suppose to deal with only 1 node.
var sourceWasFound = false
var index = 0
while (!sourceWasFound) {
val currentGraId = graph(index)
if (currentGraId == sourceVertex) {
var youngerSuccessorFound = false
for (indexSuccessors <- index+1 until graph.size if !youngerSuccessorFound) {
val successorVertex = graph(indexSuccessors)
if (newVertex.timestamp > successorVertex.timestamp) {
graph.insert(indexSuccessors, newVertex)
youngerSuccessorFound = true
}
}
sourceWasFound = true
}
index += 1
}
}
}
case class RgaId(id: String, timestamp: Long)
CRDT: maps
A map doesn't change its specificities in the context of CRDTs. As in the case of standalone applications, it's composed of key - value pairs. Among the CRDT maps we can distinguish:
- Observed Remove Map (OR Map) - this map shares the same semantics as ORset, i.e. where the elements can be added and removed any number of times and the adds always win. In the case of concurrent update, the 2 new values are merged.
- Grow-only map (GMap) - as for the case of other grow-only structures, also in this one we can't undo the state. That said, once the key-value pair is added, it can't be removed. Similarly to OR Map, when the keys are with different values in several datasets, the values are merged into a single one.
- Last-write wins Map (LWW Map) - it's a OR Map with the values of Last-write Wins Register (LWW Regiter) type. Thus in the case of conflicting writes, the most recent write is always kept.
Below you can find some test cases for CRDT maps with the use of Akka Distributed Data module:
class MapCrdtTest extends FlatSpec with Matchers {
implicit val system = ActorSystem("responses-learner-service")
private val Node1 = Cluster(system)
private val Node2 = Cluster(system)
"LWW Map" should "take last written value for a key" in {
val key = "was_read"
val lwwMapNode1 = LWWMap.empty.put(Node1, key, true)
val lwwMapNode2 = LWWMap.empty.put(Node2, key, false)
val mergedLwwMap = lwwMapNode1.merge(lwwMapNode2)
// false is written after true, so it's the most recent one
mergedLwwMap.get(key).get shouldBe false
}
"OR Map" should "merge concurrent updates" in {
val orMapNode2WithA = ORMap.empty.put(Node2, "visits_count", GCounter.empty.increment(Node1, 10))
val orMapNode1WithA = ORMap.empty.put(Node2, "visits_count", GCounter.empty.increment(Node2, 5))
val mergedOrMap = orMapNode2WithA.merge(orMapNode1WithA)
// The ORMap value type is ReplicatedData so the result of the merge relies on the merge
// method implementation of underlying type
mergedOrMap.get("visits_count").get.getValue.intValue() shouldEqual 10
}
}
CRDT are not limited to only simple data types. As shown in this post, they also apply to more complicated structures as graphs and maps. However in some cases the number of supported operations is restricted. It's the case of monotonic DAG which doesn't work well with the removals. Other graph structures solve this problem but in the other side the solution based on tombstones can lead to problem spaces (and the purge would require the synchronisation mechanism). It's much simpler for the case of flags where the true flags are always taken in precedence. Similar strategy is used to LWW Map where the last value is always kept. Other maps, as GMap, follows the same principle as monotonic DAG and they don't support removals.
