ACID is a well-known acronym for almost all developers growing with the RDBMS as the main storage. However with the popularization of NoSQL and distributed computing, another ACID acronym appeared - ACID 2.0.
This post focuses on this another ACID-like acronym. The first part explains the CALM theorem that is strictly related to the ACID 2.0. Only the next part talks about ACID 2.0 principles. The last section gives an example of its use.
CALM
Shortly speaking, the difference between ACID and ACID 2.0 is expressed in the targeted properties. The first acronym focuses on correctness and precision (for reminder, it means: Atomicity, Consistency, Isolation, Durability). The latter one is more about flexibility and robustness because it means: Associative, Commutative, Idempotent and Distributed. But before we develop these points, let's stop a moment and focus on another acronym being the departure point for ACID 2.0 - CALM.
CALM means Consistency As Logical Monotonicity. It's a theorem relating the monotonic logic to the data consistency in distributed environments. The monotonicity is used here to determine if given programs are safe under eventual consistency or not. In the latter case it means that the consistency must be strengthened.
As you can see, the monotonic is a keyword of CALM. What does it mean ? A monotonic operation is the operation that adds new data to the input and, in consequence, it can only increase or decrease the output (the output grows in only 1 direction). Any monotonic program can be then eventually consistent without any additional coordination points. Among the monothonic operations we can distinguish: variables initialization to specific value or data accumulation inside collections. In the other side we can classify as not monothonic the operations like: variable overwrites or removals from collections.
And this CALM theorem encompasses ACID 2.0 that will be explained in the next section.
ACID 2.0 explained
As already explained, the letters in ACID 2.0 means Associative, Commutative, Idempotent and Distributed but more concretely everything is about:
- Associative - the order of function execution doesn't matter. It means that in the following case both executions are equal: f(a,f(b,c)) = f(f(a,b),c). In the real world an example of that can be a not linked set where set.add(a).add(b).add(c) is the same as set.add(b).add(c).add(a) (or any other order).
- Commutative - this property is similar to the previous one except it's related to the function arguments. It means that these arguments are order-insensitive, so f(a, b) = f(b, a). A popular example illustrating it is the max function for which max(1, 2) is the same as max(2, 1).
- Idempotent - the idempotency means that the function always, even if it's called multiple times, returns the same result, such as: f(f(f(x))) = f(x). A great example of the idempotency is a put operation in a map: map.put("key1", "value1").put("key1", "value1") will always result in a single one map entry "(key1", "value1").
In the distributed computing the idempotency opens the possibility of at-least once delivery that is less expensive and easier to achieve than the at-most once one. - Distributed - its meaning is mainly symbolical. It highlights the fact that the ACID 2.0 applies on the distributed systems.
An example of ACID 2.0 implementation areConflict-free Replicated Data Types. They bring a lot of benefits. One of them is the separation of the consistency concerns. With ACID 2.0 and CRDT the data store doesn't need to enforce strong consistency. Instead it's the application layer that ensures the data and operations consistency by, for instance, semantic guarantees. One of semantic guarantees examples can be found in the G-Counter (grow-only counter) data structure that by definition can keep only incremented values. Next this counter, throughout the merge operation, computes final value that can be safely pushed to the data store. That also brings the flexibility in terms of reading and writing strategies. In additional, ACID 2.0 throughout CALM theorem is also a good indicator to tell if given data structure is a good candidate for an eventual consistency or not.
ACID 2.0 example
To see the ACID 2.0 in action we'll use the example of already quoted G-Counter to track the number of reads of given blog post. This kind of counter is here a good candidate since it's not possible to discard the fact that somebody has read the post (monotonicity). For the sake of simplicity the example is given as 2 schemes. The first one presents the counter example in the environment using the external synchronization mechanism. The second one is about a counter with G-Counter data structure. Let's start with the former one:
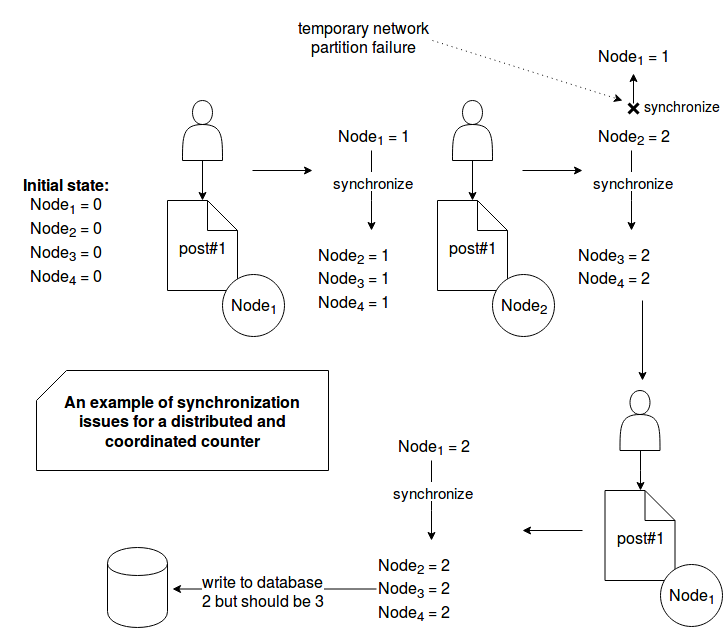
The picture above shows how a network partition can negatively impact the system consistency. Because of it, the counter on Node1 is not synchronized with the remaining ones. The next blog post read on this node increments the local counter that in its turn synchronizes with the other nodes. Sure, the coordination mechanism is very rudimentary since it ignores replication errors. Hence an additional synchronization effort is required in order to enforce the consistency. But an alternative to this solution exists and it can be a G-Counter (you can learn more about it in the post about Conflict-free Replicated Data Type):
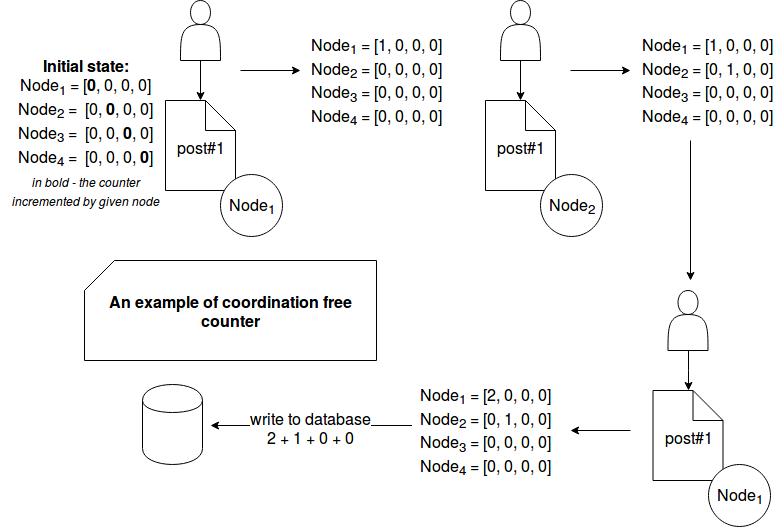
In the coordination free counter the nodes work in separation and only at one moment, when the result must be persisted to a long-term storage, they're used all together. Here the problem of network partition failure doesn't exist during the writes because only the local counters are incremented. A problem could happen though at the moment of writing. One of nodes could go down. It's why we could add an asynchronous replication between nodes to still guarantee pretty accurate results (in G-counter the max for each index is taken as the final value). It was not added in the picture in order to keep it simple and focused on difference between coordination-based and ACID 2.0 structures.
As told in the first section, the ACID 2.0 concept has nothing in common with classical ACID that we know from RDBMS. The former one is reserved to the distributed environments and helps to guarantee eventual consistency without any additional coordination mechanisms. The main point of ACID 2.0 is CALM and the monotocity principle where the output can only grow. An example of so growing output is grow-only counter. It was described in the 3rd section with 2 architectures. The first one used a a synchronous replication mechanism and as we could see, it led to some inconsistent results. The second one used coordination-free mechanism that should guarantee much better (performance and consistency criteria) results for this specific use case.
