https://github.com/bartosz25/spark-.../bipartite/BipartiteGraphTest.scala
When I was analyzing the API of Gelly, I was quite surprised for its support of bipartite graphs. First, because I didn't know that data structure and second because it wasn't supported in other analyzed frameworks. Hence, I added that graph structure to my backlog and sometime later wrote a post to explain it better.
In the first part of this post I will present the basics of bipartite graphs. This part will contain a short theoretical explanation and also some of the use cases. The second part will present an implementation of a recommendation algorithm with Apache Spark GraphX and a bipartite graph.
Bipartite graphs definition
A bipartite graph is a graph whose vertices can be divided into 2 disjoint datasets. The edges in a bipartite graph are allowed only across these datasets, i.e. 2 vertices can't be joined inside the same dataset. It's then a natural way to model the relationship between 2 different entity types, like users and items in an e-commerce store.
There are a lot of other different use cases of bipartite graphs. They were employed to model unemployment in a job market, task scheduling, assignment of students to lessons and finally as a base of recommendation systems. The bipartite graphs were very often proposed as a solution to Netflix recommendation system challenge in 2009. I will detail this use case in the next section.
Aside from these use cases, bipartite graphs also have some important properties. The first of them is perfect matching. It occurs when each node has exactly one edge incident on it. Another interesting property, still related to the matching, is maximum matching. A simple matching is only the definition of a relationship between the vertices of both datasets. The maximum matching is therefore the maximal number of edges that we can create between the vertices of both datasets. We can use this property to solve the problem of job scheduling optimization.
Bipartite graphs - recommendation example
The special branch of the recommendation systems using bipartite graph structure is called collaborative filtering. Basically, this approach uses the interactions between users and items to find out the item to recommend. Most of the time, it ignores the users and items attributes and only focuses on the relationship between 2 datasets. That problem can be then formulated as a link prediction problem because the goal is to guess which new edges could be generated between the subgraphs of users and items.
The collaborative filtering has 2 categories. The first one is user-based, i.e. it measures the similarity between users in order to get the items to recommend. The second category is item-based and it measures the similarity between items. The collaborative filtering has then a strong assumption about users because the model assumes that similar users will like similar items.
A very common representation of the collaborative filtering uses utility matrix where each cell represents the opinion of given user for the specific item. For instance, the cell can say how much a user liked given item. However, the matrix has one important drawback. It needs a lot of space (n*m where n is the number of users and m the number of items). That's why I tried, as an exercise, to implement the collaborative filtering on a bipartite graph with the algorithm proposed in "Network-based recommendation: Using graph structure in user-product rating networks to generate product recommendations" article.
The model uses 2 formulas. The first one computes the weight between 2 users. The weight can be considered as the similarity measure because it takes all n products common for both users:
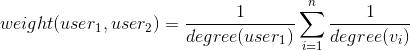
The second formula computes the similarity score between a user and an item, based on the user's neighbors who interacted with the item:
For the sake of simplicity, I used an in-memory key-value store to hold the users' weights. Exactly for the same reason, I also divided the processing into 2 major parts. The former one computes the weights whereas the latter the recommended products. Unlike the model from the paper, I omitted the computation of the items already known by the users. That's why you will see here different values for them. And since the code is quite long, let's start by the graph definition:
private val vertices = testSparkContext.parallelize(
Seq(
// Top vertices
(1L, 0), (2L, 0), (3L, 0),
// Bottom vertices
(100L, 0), (101L, 0), (102L, 0), (103L, 0), (104L, 0), (105L, 0)
)
)
private val edges = testSparkContext.parallelize(
Seq(
// Vertex A
Edge(1L, 100L, 1), Edge(1L, 101L, 1), Edge(1L, 102L, 1),
// Vertex B
Edge(2L, 101L, 1), Edge(2L, 103L, 1),
// Vertex C
Edge(3L, 102L, 1), Edge(3L, 103L, 1), Edge(3L, 104L, 1), Edge(3L, 105L, 1)
)
)
private val graph = Graph(vertices, edges)
Nothing hard to understand. A simple bipartite graph with top and bottom vertices. Please notice that it's only the basic part because at the beginning the graph is transformed into an enriched graph:
val verticesWithDegree = graph.triplets.groupBy(triplet => triplet.srcId)
.map {
case (userVertexId, edges) => (userVertexId, edges.size)
}
val graphWithDegreeDecoratedVertices = Graph(verticesWithDegree, edges)
Here too, everything is simple. I just computed the number of outgoing edges (degree) for all vertices. I will use this value later in both formulas. Now, I will compute a part of the first formula by creating a list of neighbors with their degrees and the common item degree:
case class NeighborsAttributes(user1Degree: Int, user2Degree: Int, itemDegree: Int)
val neighborsEdges = graphWithDegreeDecoratedVertices.triplets.groupBy(triplet => triplet.dstId)
.filter {
case (_, triplets) => triplets.size > 1
}
.flatMap {
case (itemVertexId, triplets) => {
val materializedTriplets = triplets.toSeq
val itemDegree = materializedTriplets.size // degree(v_i)
val users = materializedTriplets.map(triplet => triplet.srcId)
val usersDegrees = materializedTriplets.map(triplet => (triplet.srcId, triplet.srcAttr)).toMap
// build uw pairs
users.combinations(2)
.map(neighbours => Seq(
Edge(neighbours(0), neighbours(1), NeighborsAttributes(usersDegrees(neighbours(0)),
usersDegrees(neighbours(1)), itemDegree)),
Edge(neighbours(1), neighbours(0), NeighborsAttributes(usersDegrees(neighbours(1)),
usersDegrees(neighbours(0)), itemDegree))
))
.flatten
}
}
This triplet will help me to compute the weights of neighbors and save them into my fake key-value store:
object RecommendationFunctions {
def computeNeighborsWeight(commonItemsWithUserDegrees: Iterable[Edge[NeighborsAttributes]]) = {
var user2Degree = 0d // ==> neighbor edges
var srcUserEdges = 0d
var commonItemsSum = 0d
for (commonItem <- commonItemsWithUserDegrees) {
srcUserEdges = commonItem.attr.user1Degree
commonItemsSum += 1d/commonItem.attr.itemDegree
user2Degree = commonItem.attr.user2Degree
}
val neighborWeight = 1/srcUserEdges * commonItemsSum
NeighborWeightWithDegree(neighborWeight, user2Degree.toInt)
}
}
case class NeighborWeightWithDegree(weight: Double, neighborDegree: Int)
object UsersWeightsStore {
private val weights = new ConcurrentHashMap[String, NeighborWeightWithDegree]()
def all = weights
def addWeight(user1: Long, user2: Long, attribute: NeighborWeightWithDegree) {
weights.put(s"${user1}_${user2}", attribute)
}
def debug = println(s"weights=${weights}")
}
neighborsEdges.groupBy(edge => (edge.srcId, edge.dstId))
.foreachPartition(partitionData => {
partitionData.foreach {
case ((srcUser, dstUser), attributes) => {
val neighborsWeight = RecommendationFunctions.computeNeighborsWeight(attributes)
UsersWeightsStore.addWeight(srcUser, dstUser, neighborsWeight)
}
}
})
At this moment I have all the neighbors weights of the graph. And it was not easy. Computing the items to recommend also requires some effort. First, I will compute the weighted value of the items linked to the neighbors:
val weightedValuesPerProduct = graphWithDegreeDecoratedVertices.triplets
.flatMap(triplet => {
import scala.collection.JavaConverters._
val neighbors = UsersWeightsStore.all.asScala.filter(entry => entry._1.contains(s"${triplet.srcId}_"))
neighbors.map(entry => {
val neighborId = entry._1.split("_")(1).toLong
val userNeighbor = entry._2
val weightedValue = userNeighbor.weight * (1d/userNeighbor.neighborDegree.toDouble)
(neighborId, triplet.dstId, weightedValue)
})
})
As you can see, I take all neighbors for every edge between a user and an item, and retrieve all similar items reviewed by them to compute a part of the final's formula sum. And finally, I use all of this to compute the final suggested products:
val recommendedProducts = weightedValuesPerProduct.groupBy {
case (neighborId, _, _) => neighborId
}.mapPartitions(userSimilarProducts => {
RecommendationFunctions.computeRecommendedProducts(userSimilarProducts)
})
val recommendationResults = recommendedProducts.collect
val user1Recommendations = recommendationResults.filter(userItems => userItems._1 == 1L)
user1Recommendations(0)._2 contains allOf((101,0.083), (102,0.042), (103,0.125), (104,0.042), (105,0.042))
val user2Recommendations = recommendationResults.filter(userItems => userItems._1 == 2L)
user2Recommendations(0)._2 contains allOf((100,0.083), (101,0.083), (102,0.146), (103,0.063), (104,0.063), (105,0.063))
val user3Recommendations = recommendationResults.filter(userItems => userItems._1 == 3L)
user3Recommendations(0)._2 contains allOf((100,0.042), (101,0.104), (102,0.042), (103,0.063))
def computeRecommendedProducts(userSimilarProducts: Iterator[(VertexId, Iterable[(VertexId, VertexId, Double)])]) = {
userSimilarProducts.map {
case (userId, productsWeights) => {
val userTopProducts = productsWeights.groupBy {
case (_, itemId, _) => itemId
}.map {
case (itemId, products) => {
val weightedValueSum = products.map {
case (_, _, weight) => weight
}.sum
(itemId, BigDecimal(weightedValueSum).setScale(3, BigDecimal.RoundingMode.HALF_UP).toDouble)
}
}
(userId, userTopProducts.toSeq.sortBy(itemWithValue => itemWithValue._1))
}
}
}
The exercise was quite painful and when I compared the result with some of Python implementations of matrix-based collaborative filtering, I knew that my code could be only used to illustrate how hard is to implement recommendation algorithms in bipartite graphs. It doesn't mean that this structure doesn't fit well to the problem though. In one of the next posts, I will try to implement the same algorithm with the use of a streaming approach to get a better idea. Meantime, if you would like to play with the bipartite graphs and the collaborative filtering, there are many of the Open Source implementations, like implicits quoted in "Read more..." section, that is much more intuitive in use.
