During last weeks we've discovered a lot about graph data processing in distributed world. However we haven't learned yet about the problems the graphs can solve. And it's as important as the knowledge about the processing techniques. Hopefully, this post will try to catch up this late.
This post is the first from the series devoted to graph algorithms in a distributed world. Most of them will be presented in a vertex-centric approach because of its popularity in modern frameworks. Today we will learn about: PageRank, connected components and Single Source Shortest Path (SSSP). Each of them will be illustrated with an execution schema. Since we're not discussing vertex-centric frameworks yet, we won't show their implementation in the code.
PageRank
PageRank is an algorithm popularized with the success of Google. The algorithm addresses the problem of the authority of vertices in the graph. Its goal consists of telling whether some of them are more powerful than the others. This power translates to the likelihood that a person reaches given vertex by randomly walking in the graph. In Google's context it means the likelihood of clicking randomly on a link. But the search engine is not a single use case of PageRank. It can be also used in:
- recommendation systems - Twitter used its variation called Personalized PageRank to suggest accounts to follow (TwitterRank). It was also used in Netflix-and Amazon-like recommendations based on user notes. This PageRank's variance is called ItemRank.
- anomaly detection - a variation called MonitorRank proposes a solution for such problems.
- general authority detection - in the past PageRank and Reverse PageRank were used to represent the most important functions in Linux kernel. It helped a lot to automatically discover key components among 15 millions of lines of code and 300 000 functions. Another authority detection was BookRank - a PageRank applied to books world.
- prediction - PageRank was used to predict traffic flow and human movement in the road and urban spaces systems.
The PageRank for each vertex is computed as follows:
The algorithm was born from the random surfer model where the "surfer" always follows the outgoing edges. However, at some point, he can become "bored" about that and can start clicking on random pages. PageRank introduces a damping factor (d in the above formula) to represent the probability that the surfer will continue to click on outgoing links. N in the equation represent the total number of vertices while L the number of outgoing edges for each vertex related to the vertex whose PageRank we're computing. To see how it works in a vertex-centric model, there is an example:
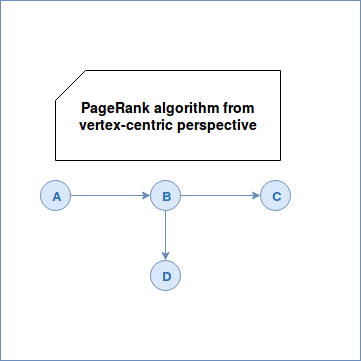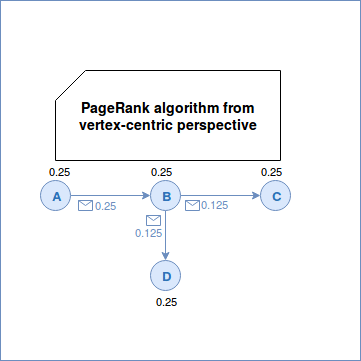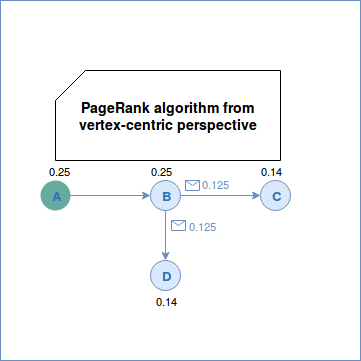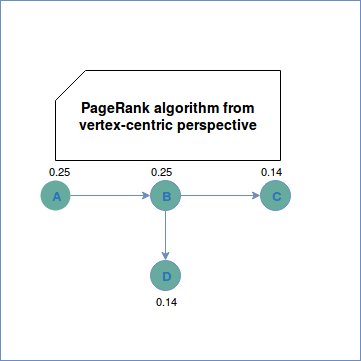
Connected components
The second of presented algorithms is able to group similar vertices and it's called connected components. A connected component is a subgraph whose vertices are pairwise disjoint. The union of connected components represents all vertices in the graph. The vertices stored in each subgraph don't connect to the vertices from other subgraph and they can be considered as graph partitions. Partitioning is, by the way, one of the use cases of connected components. Among others, we can also distinguish community detection in social graphs.
The implementation of this algorithm is quite straightforward. Please notice however that it applies to undirected graphs. Directed ones are computed with the Strongly Connected Components algorithm.
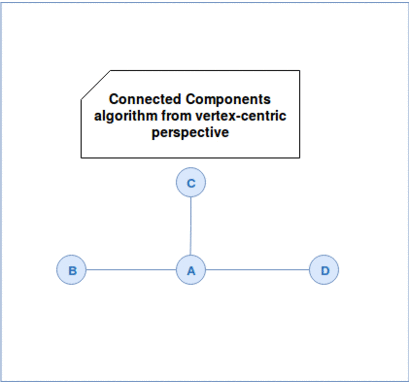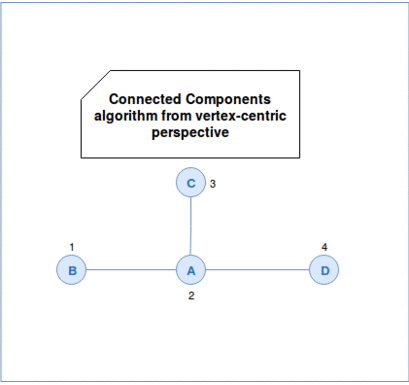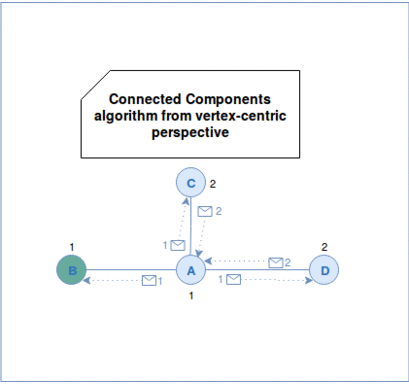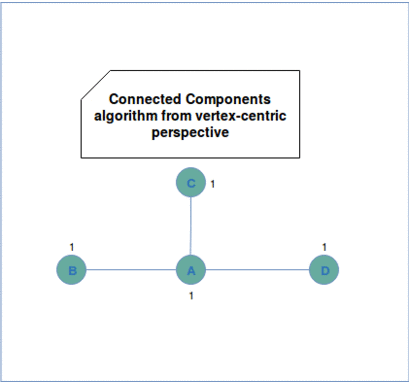
The algorithm itself starts by assigning unique ids to each vertex. In the first superstep the vertices send their ids to their neighbors. Every neighbor verifies later whether the minimal id among received ones is lower than its own id. If it's the case it overrides its id and propagates this information to its neighbors. The iteration continues as long as there are vertices changing their ids. We can see this workflow in the following animation:
Single Source Shortest Path
The last algorithm presented here is responsible for finding the shortest path between 2 vertices in a graph. The "shortest" means here the minimization of the sum of edges weight. The weights can represent physical distance but they can carry also different information. Among the problems the shortest path tries to solve we can quote finding the shortest physical distance between 2 points in a map, the quickest way to send packets in a network or finding the degree of separation between people in social network.
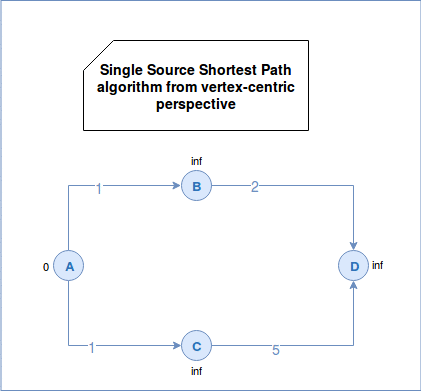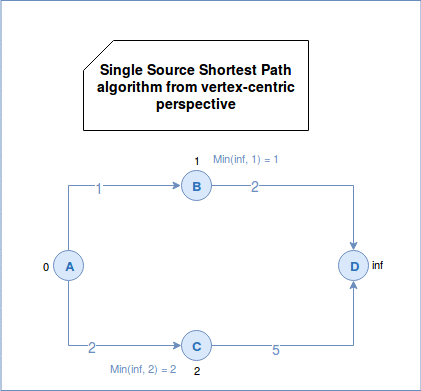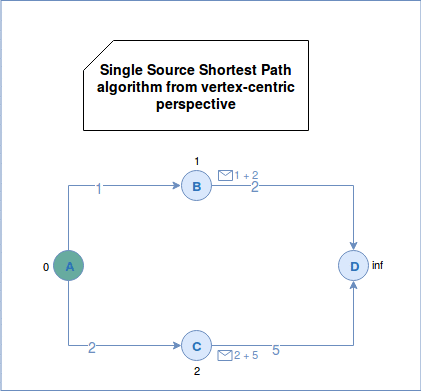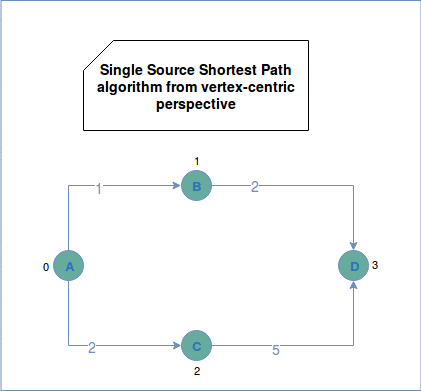
Popular algorithm solving SSSP problem is Djikstra. First, it initializes the values of all vertices to positive infinity except the root vertex that has a distance of 0 to itself. The root vertex is the starting point of the iteration and the only known vertex at the first superstep. Later the algorithm sends the sum of vertex distance and edge weight to all neighbors. The neighbors takes the minimal value among their current value (by default: positive infinity) and the minimal value of the sent messages. The algorithm terminates when there are no more active (not traversed) edges.
In a vertex-centric approach we can represent the SSSP problem as:
PageRank, connected components and SSSP are graph algorithms that can be easily solved with vertex-centric paradigm. Some of them, aside of bringing business insight, can also be used as pre-processing steps in the graph, especially for partitioning. Hopefully, with the vertex-centric model we can do a lot more. It's why stay tuned for the next posts illustrating graph algorithms designed from the vertex perspective.
