Until now we've discovered exclusively the concepts devoted to computing distributed graphs. But the compute part can't go without storage. And since for the latter in the context of graph we can't talk about the storage, it requires its own detailed explanation.
Data Engineering Design Patterns

Looking for a book that defines and solves most common data engineering problems? I wrote
one on that topic! You can read it online
on the O'Reilly platform,
or get a print copy on Amazon.
I also help solve your data engineering problems 👉 contact@waitingforcode.com 📩
Three sections compose this post. The first one tries to highlight the difference between graph processing and graph database. The second part provides an insight into different graph data storage techniques. The final section gives some examples of graph databases implementing the concepts from previous section.
Graph database vs graph processing
In the recent posts we've focused mainly on the graph processing. For most of the frameworks implementing these concepts, the data is stored in the framework-specific format, partitioned and loaded into workers memory before processing.
In the other side, a graph database is a storage system saving the data with graph structures such as vertices or edges. If we should compare both graph concepts to data processing concept we've learned until now, we could consider graph processing as Apache Spark and graph database as mutable sources for the data processing logic.
Graph database is a category of NoSQL databases. We can describe it with 4 components: storage, querying facility, scalability and transaction processing. Since I'll describe the storage in the remaining part of this post, I'll discuss here only 3 last points:
- querying facility - like any other database, graph databases also have their querying languages. Among popular languages, we can find Cypher (Neo4j, declarative language, similar to SQL) and Gremlin DSL (Apache TinkerPop, procedural language). Graph databases support its own query types: point querying (direct querying by an attribute as for instance vertex property), subgraph and supergraph queries (all kinds of traversal, for example Breadth-First Search, Depth-First Search).
- scalability - this point strongly connects with graph partitioning that, as you've already learned, is not an easy task in the context of graphs. The good graph partitioning should minimize the number of edges connecting vertices located on different machines as much as possible to exploit the locality character of the graph and reduce the network communication. Theoretically, it's possible to achieve this result. The problem is graph evolution that can break the most perfect partitioning very quickly.
One approach to deal with partitioning problem is … to not partition at all. Neo4j, a popular graph database, organizes the data in master-slave architecture where all writes are replicated to slaves. With the range queries it's then possible to run chunks of data on each machine and aggregate partial results at the end. - transaction processing - depending on the underlying database, it can be either ACID or BASE (strongly vs eventually consistent). As you'll see in the next part, some of the graph databases use a key-value storage and inherit their consistency characteristics directly from there.
Storing graph data
Graph data has specific, often continuous structure. Vertices are linked together through edges and at first glance, we could think that it's represented as one big file for each subgraph. However, it's not the case and graph can be represented with the help of different data structures:
- adjacency matrix - this structure uses a bi-directional matrix of boolean values to represent the links between vertices. Each dimension has a list of all vertices ids and if 2 vertices are connected, their value is set to true:
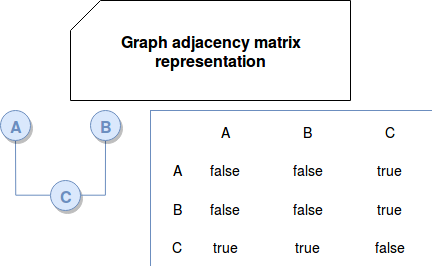
In this structure, it's easy to figure out if 2 vertices are connected. It's also easy to add or remove vertices. But it's not space efficient - especially if a graph is sparse (few edges). Another drawback is the execution of traversal queries because it requires to read all vertices to find all neighbors of the traversed vertex. - incidence matrix - this solution also uses bi-directional matrix but it represents vertices and edges with integers values. Incidence matrix stores vertices as rows and edges as columns. If an edge is not connected to given vertex, their value is set to 0. Otherwise, the value corresponds to the number of legs of the given edge connected to the specific vertex. Most of the time the value will be 1 but sometimes for loop edges, it'll be 2. In the case of a directed graph, -1 value represents incoming edge:
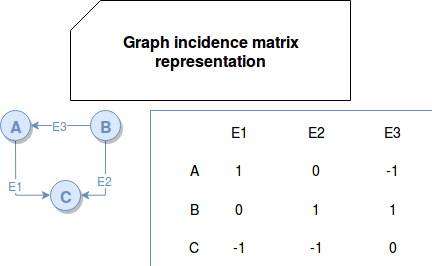
The drawbacks of this representation are similar to the ones of adjacency matrix - space inefficiency and the execution time. - adjacency list - here the data structure stores all vertices in a list and for each of them it defines a list with its closest neighbors:
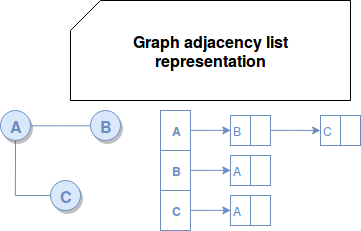
From space efficiency point of view, this solution performs better than 2 previous ones based on matrices. Moreover, with compression techniques, it can considerably optimize the used storage. It's also a better choice for traversals since we can get the list of neighbors immediately. But in the other side, it performs worse for vertices connectivity check because in the worst case it needs to iterate over all the records in the list of one of the analyzed vertices. The same query executes in constant time for the adjacency matrix. - edge table - this structure is a table where one column corresponds to target vertex id and another to destination vertex id. The organization is then similar to adjacency matrix except only the connected vertices are stored.
- index-free adjacency - the last and the most recent structure was popularized by Neo4j in its paper about native and non native graphs . In this structure the vertices are physically connected according to their edges. They contain the references to their incoming and outgoing neighbors (hence forward and backward arrows in the following schema). This natural way of graph representation helps to improve traversals and its execution time is proportional to the graph size. However it makes the horizontal scalability even more challenging.
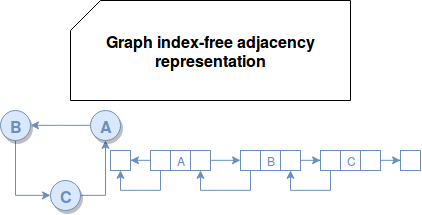
Native or not native graph databases
In the blog post "Graph Databases for Beginners: Native vs. Non-Native Graph Technology" quoted in Read also section, Neo4j proposes a distinction for technologies storing graphs. They classify graph storages as being native and not native. The first approach is characterized by "graph-first" citizenship. Concretely it means that the graph data is stored as a...graph. Not-native graph technology is the one which delegates the storage to 3rd party storages as key-value stores or relational databases.
The proposed differentiation point is the use of index-free adjacency by the storage technology. Accordingly to the post, this structure is the most natural way to represent graph structures in the storage part.
Above list contains only some of the main storage structures. There are also different engines able to store graph data:
- native graph storage - the data is stored as graph parts: vertices and edges. Thanks to that they're good candidates for all graph-specific operations as traversals. The problem with them is a worse adaptation for random-access queries. Although some of the implementations try to overcome this issue by storing graph alongside with an index.
- NoSQL storage - here the graph components are stored by key-value stores as HBase or document-oriented stores. Such storage usually performs good for single hop queries but is less efficient for deep graph traversals. Even if we store the graph as an adjacency list in a key-value store, to traverse the vertices we'll always need to: retrieve all edges of currently read vertex and make the query on them to find their edges, and so on. The number of key-based lookups will be then equal to the number of all vertices met during the traversal.
- relational database - yes, even though this solution is difficult to implement and maintain, the graph solutions based on relational databases exist. Modeling graph traversal in SQL is quite difficult because we can't predict the depth of the traversal in advance. Moreover, if it would be somehow possible, in SQL we would use plenty of JOINs that at some point may become an unbeatable bottleneck.
- multi-model database - this approach is able to store the same data in multiple different forms, e.g. as documents or graphs. This single storage system provides consistent data governance and access. The storage strategy depends on the implementation but a lot of them store graph as a native graph.
Graph databases - examples
Until now we've discovered only theoretical concepts about the storage of graph data. But to not let us hungry, let's try to find the implementations of these ideas. Maybe the most famous implementation of native graph storage is Neo4j. It stores data in files where each of them is responsible for different graph property (vertices, edges, labels, attributes …). The vertices have a fixed size of 9 bytes and thanks to that they can be accessed faster. The beginning of given vertex is computed as 9 * vertex index. The same fixed-size rule concerns edges represented as a doubly linked list. To guarantee traversal performances, each edge stores the pointers for previous and next edges of the source and destination vertex.
An example of storage using NoSQL technologies is JanusGraph. This Open Source project stores graph data as an adjacency list with all edges (not only the pointer) in one of the provided stores: Apache Cassandra, Apache HBase or Google Bigtable. Another graph database using NoSQL is DGraph that is based on Badger - a key-value store implemented in Go. Badger is used as an inverted index to store all outgoing edges of vertices sharing the same predicate.
Regarding to multi-model database we can quote OrientDB as an example. It comes with 2 APIs: one for document-oriented storage and another for graph-oriented storage. The latter is built on top of the former one. As JanusGraph, it stores the graph in the form of an adjacency list. But the list is completed with document database capabilities to store physical vertices.
An example of graph storage from the family of relational databases is SQL Server 2017. It stores graph data in 2 tables: one for vertices and another for edges.It supports traversals through MATCH statement.
The article showed how the graph data can be stored with different structures. The simplest data representation are matrices with values representing vertices connectedness. More complicated ones are linked list and among them a doubly linked list implemented in Neo4j that by the way provides a classification of graph databases on native and not native. Everything that shows clearly that distributing graph storage, mainly because of its connected character, is quite challenging. As illustrated in the 3rd part of the post, horizontal scalability is most of the time provided with NoSQL key-value stores, used in JanusGraph and DGraph projects.
Consulting

With nearly 16 years of experience, including 8 as data engineer, I offer expert consulting to design and optimize scalable data solutions.
As an O’Reilly author, Data+AI Summit speaker, and blogger, I bring cutting-edge insights to modernize infrastructure, build robust pipelines, and
drive data-driven decision-making. Let's transform your data challenges into opportunities—reach out to elevate your data engineering game today!
👉 contact@waitingforcode.com
🔗 past projects


