Use cases of streaming surprise me more and more. In my recent research about graph processing in Big Data era I found a paper presenting the graph framework working on vertices and edges directly from a stream. In case you've missed that paper I'll try to present this idea to you.
A virtual conference at the intersection of Data and AI. This is not a conference for the hype. Its real users talking about real experiences.
- 40+ speakers with the likes of Hannes from Duck DB, Sol Rashidi, Joe Reis, Sadie St. Lawrence, Ryan Wolf from nvidia, Rebecca from lidl
- 12th September 2024
- Three simultaneous tracks
- Panels, Lighting Talks, Keynotes, Booth crawls, Roundtables and Entertainment.
- Topics include (ingestion, finops for data, data for inference (feature platforms), data for ML observability
- 100% virtual and 100% free
👉 Register here
As for almost every new idea, this post starts with a section containing its definition. The next part shows how streaming-based graph processing was implemented in X-Stream (do not confuse with XStream which is a library for XML serialization). Finally in the last section I'll propose a reengineering of X-Stream architecture the help of Apache Kafka and Apache Cassandra.
Streaming graphs
In stream-based graphs the data source is a stream. It can contain values in one of the following forms:
- edges and vertices in 2 distinct streams - however this representation is rarely practical since we'll need to join both streams and as shown in the posts about Apache Spark Structured Streaming joins, joins in streaming are not easy. Moreover, it goes against the main reason to use streams in graph-oriented computations - space efficiency - that will be explained later in this post.
- triples - here the stream stores a triplets composed of: source vertex, destination vertex and an edge linking them. All 3 elements can store their values. But here too we encounter a problem because it's difficult to solve conflicting situations where the values are unknown or they change between subsequent operations on given vertices.
- edges - in this situation the stream stores only the edges. A different storage is responsible for storing vertices. As you can see, it's a similar approach for the previous except this one doesn't have a problem of "desynchronized" values. Processing frameworks using edges as input data belong to the category of edge-centric computation model.
The algorithms based on streamed graphs may implement different execution models. The first one is incidence streaming. It processes all edges connected to the same vertex at the same time. They appear one after another in the input stream. Unfortunately this practical approach isn't universal because not all graphs can be formatted so.
Another model based on streams is called semi-streaming. Why semi ? It's because it's different from the classical data stream model. The latter one processes data from input stream by putting it into the memory. But very often the amount of memory is limited and some more space-efficient solutions are required. One of them is semi-streaming model. It's based on 2 principles. First, it forbids random access - graph data is processed in arbitrary order. Second, it limits algorithm's memory to O(n * polylog(n)) bits (or in simpler terms: O (n logkn for some constant k), where n is the number of graph vertices. Polylog effectiveness in graph context means that there is enough space to store vertices but not enough to keep all edges in memory. It fits well for many real world graphs where the number of edges is much bigger than the number of vertices (|V| << |E|). In the other side, it's not adapted for sparse graphs with few edges (e.g. trees). Researchers used semi-streaming model to solve different problems with graphs: connectivity, bipartiteness, matching or shortest-path. The solutions for 2 last problems are the approximations and from that we can consider semi-streaming model as not completely adapted for all graph traversal-related problems.
X-Stream
One of implementations of graph streaming approach is X-Stream library developed at Swiss EPFL research institute. The framework follows edge-centric approach where the edges are the input data. It has also the specificity to not being distributed. X-Stream uses local memory and disk storage to the processed entries. Instead of using multiple nodes it benefits from multiple CPUs to distribute the workload.
Two phases compose the execution:
- Scatter - it applies used-defined function to the source vertex of each processed edge. The result of the function determines whether the destination vertex of the relationship must be updated. If yes, an update is put into an update list.
- Gather - this phase reads all vertices and eventually applies the updates from scatter stage on each of them. Despite its single-node character, the input data in X-Stream is partitioned. Scatter can generate updates for destination vertices located on other partitions. It's why before the gather phase begins, the program must move the updates to appropriate partitions.
As you can imagine, the execution is iterative and after each gather phase a new scatter one begins with already updated vertices values. All manipulated data is stored first in a memory buffer representing the partition of scatter phase. Later it's moved to the buffer storing vertices for gather phase.
Unintentionally I needed to introduce the idea of partitions to explain both phases better. Let's stop a while to focus on partitions. As in the case of other data sources, a partition for an X-Stream program is a unit of parallelization. Each stream partition stores: a set of mutually disjoint vertices (= their union must produce all vertices of the graph), a list of edges whose source vertex is in the list of vertices and an update list with all updates to apply to partition vertices. The number of partitions is chosen to maximize I/O and if you're curious, the formula is given in the "X-Stream: Edge-centric Graph Processing using Streaming Partitions" paper quoted in Read also section.
However X-Stream is not a solution for all problems. Its big drawback is exclusively vertical scalability and because of that the framework is limited by the metrics related to that scalability : I/O bandwidth and storage place. An alternative called Chaos was proposed from these findings. Once again the researchers of EPFL contributed to its development. Unlike X-Stream, Chaos is a distributed data processing framework composed of 2 sub-systems: storage and computational. The concept of streaming partitions is also present. The difference is that the formula to compute them is different: k * number of machines. Hence each machine is responsible for k partitions. Data stored in partitions is the same as for X-Stream, i.e. vertices set, edges and updates list. Regarding to the computation, Chaos also executes in Scatter-Gather mode.
X-Stream with Apache Kafka
After reading both papers quoted in the "Read also" section I wanted to do an exercise and adapt the ideas from X-Stream to nowadays distributed tools. But before showing this proposal, some assumptions from the paper. The article assumes that the number of partitions stays fixed throughout the computation. It also formalized scatter and gather algorithms as (standalone version using disk and memory):
# scatter
for each streaming partition s
while edges left in s
load next chunk of edges into input buffer
for each edge e in memory
scatter_function(edge) appending to output buffer
if output buffer is full or no more edges
in-memory shuffle output buffer
for each streaming partition p
append chunk p to update file for p
# gather
for each streaming_partition p
read in vertex set of p
while updates left in p
load next chunk of updates into input buffer
for each update u in input buffer
gather_function(update) # update.destination - vertex receiving the update
write vertex set of p
In this exercise I tried to bring fault tolerance with the data source and it's the reason why vertices aren't stored on each computation node as it's supposed to be in semi-streaming model and X-Stream framework. So, the proposals from this section are simplified distributed versions of X-Stream.
My initial proposal to implement X-Stream was based on Apache Kafka and looked like in the following schema:
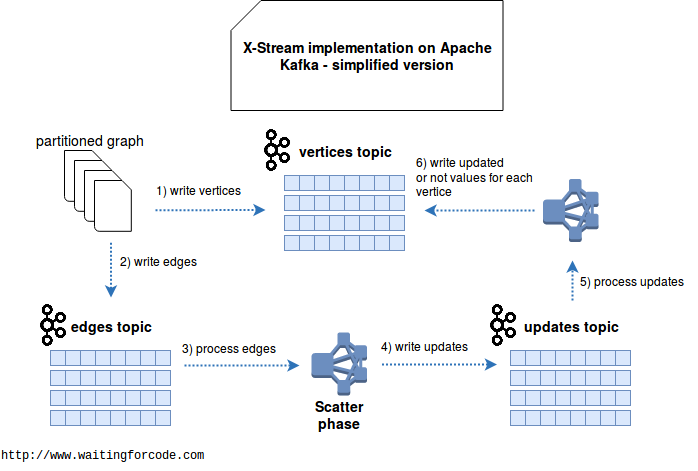
However this solution has important drawbacks. First, it's unable to update the value of edges when it can be modified after changing vertex value. Second, it requires every time to write a new complete set of vertices. Moreover, we have to have always the same consumers - otherwise we lost the last processed offset and the new consumers can reprocess the vertices from thousands of previous iterations. Finally, this implementation supposes either the updates being sent subsequently for given vertex or simply that the update function doesn't need to know all updates at the same time and it can store partial results somewhere else. This "somewhere else" place was a point that made me think about another possible architecture, based on key-value store and eliminating a lot of above drawbacks:
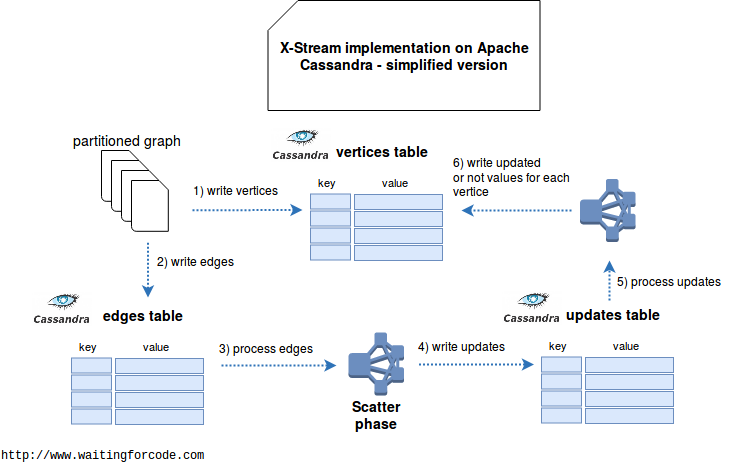
In above architecture each worker is responsible for a specific subset of vertices ids. We consider here than the ids are consequent - otherwise it would lead to skewed partitions. The iteration starts by reading all edges one-by-one and eventually generating the updates where the primary key is composed of updated vertex, worker's id and increment index at every update generated on given node. For instance it would be (100, 1_1), (100, 1_2), (100, 1_3) for 3 updates generated for vertex 100 on the node 1.
In gather step each node scans over the same subset of ids. The difference is that it queries for all updates at once to be able to compute new vertex value with them. This new value is written back to the vertices table. In the case when the vertex doesn't change, we don't waste the read operation. And eventually, if we'd need updated values on the edges side, it would also be easy to write them in the edges table.
The fault-tolerance is brings by a tracking of last processed element - the delivery guarantee is at-least-once though. But it isn't a problem under condition that the processing code is idempotent. And it is since it never manipulates source data (e.g. scatter doesn't overwrite edges table!) and always writes the same updates (no append,only in-place update).
An example of key-value-stream graph processing data structure could look like in the following pseudo-code snippet:
cqlsh> CREATE KEYSPACE graph WITH REPLICATION = { 'class' : 'SimpleStrategy', 'replication_factor' : 1 };
cqlsh> CREATE TABLE graph.vertices (
... id INT PRIMARY KEY,
... value INT
... );
cqlsh> INSERT INTO graph.vertices (id, value) VALUES (1, 0);
cqlsh> INSERT INTO graph.vertices (id, value) VALUES (2, 0);
cqlsh> INSERT INTO graph.vertices (id, value) VALUES (3, 0);
cqlsh> INSERT INTO graph.vertices (id, value) VALUES (4, 0);
cqlsh> CREATE TABLE graph.edges (
... source_vertex INT,
... target_vertex INT,
... edge_value INT,
... PRIMARY KEY (source_vertex, target_vertex)
... ) WITH CLUSTERING ORDER BY (target_vertex DESC);
cqlsh> INSERT INTO graph.edges (source_vertex, target_vertex, edge_value) VALUES (1, 2, 100);
cqlsh> INSERT INTO graph.edges (source_vertex, target_vertex, edge_value) VALUES (1, 4, 32);
cqlsh> INSERT INTO graph.edges (source_vertex, target_vertex, edge_value) VALUES (2, 3, 1);
cqlsh> INSERT INTO graph.edges (source_vertex, target_vertex, edge_value) VALUES (3, 4, 19);
cqlsh> CREATE TABLE graph.updates (
... vertex_id INT,
... node_id INT,
... update_id INT,
... value INT,
... PRIMARY KEY(vertex_id, node_id, update_id)
... ) WITH CLUSTERING ORDER BY (node_id ASC, update_id ASC);
cqlsh> INSERT INTO graph.updates (vertex_id, node_id, update_id, value) VALUES (1, 1, 1, 10);
cqlsh> INSERT INTO graph.updates (vertex_id, node_id, update_id, value) VALUES (1, 1, 2, 5);
cqlsh> INSERT INTO graph.updates (vertex_id, node_id, update_id, value) VALUES (1, 1, 3, 1);
cqlsh> INSERT INTO graph.updates (vertex_id, node_id, update_id, value) VALUES (1, 2, 1, 20);
cqlsh> INSERT INTO graph.updates (vertex_id, node_id, update_id, value) VALUES (1, 3, 1, 21);
cqlsh> INSERT INTO graph.updates (vertex_id, node_id, update_id, value) VALUES (1, 4, 1, 22);
cqlsh> INSERT INTO graph.updates (vertex_id, node_id, update_id, value) VALUES (2, 4, 1, 32);
cqlsh> SELECT * FROM graph.updates WHERE vertex_id = 1;
vertex_id | node_id | update_id | value
-----------+---------+-----------+-------
1 | 1 | 1 | 10
1 | 1 | 2 | 5
1 | 1 | 3 | 1
1 | 2 | 1 | 20
1 | 3 | 1 | 21
1 | 4 | 1 | 22
(6 rows)
cqlsh> UPDATE graph.vertices SET value = 79 WHERE id = 1;
cqlsh> SELECT * FROM graph.vertices;
id | value
----+-------
1 | 79
2 | 0
4 | 0
3 | 0
(4 rows)
Streaming model for graph processing, even though it's limited to some problems, is an interesting use case for streaming data sources. With its semi-streaming model it can be used to process big datasets in limited space. One of its first implementations, X-Stream, was able to process many real world graphs on a single machine within some minutes. This single-node computation framework evolved to improved distributed version called Chaos. Based on them I did an exercise and proposed 2 alternative fully-distributed architectures based on Apache Kafka and Apache Cassandra. They look correctly on the paper. But in the other side, they're based on some specific assumptions about the graph structure and may not fit in all the cases.
