Graph data processing, even though seems to be less popular than streaming or files processing, is an important member of data-oriented systems. And as its "colleagues", it also has some different processing logics. The first described in this blog is called vertex-centric.
The first section of this post explains the main ideas behind vertex-centric processing. The next one explores them more in details while the subsequent one talks about its important computational models. The final part gives an example of vertex-centric program written with Apache Flink's library called Gelly.
Vertex-centric graph processing
Iterative graph processing is one of the categories of graph data processing. This kind of processing consists of iterations over user-defined function. Each function's call updates or not vertices and/or edges values. The iterations stop when the algorithm reaches a satisfying threshold or simply after executing a certain number of times. Vertex-centric graph processing is one of the examples of iterative graph processing model. Please notice that other names defining it are: vertex-oriented graph processing or "Think Like a Vertex".
This computational model works in master-slave architecture where the master node is responsible for: slave workers, execution monitoring, coordination and eventually synchronization, if used, among the workers. Sometimes it may be in charge of graph partitioning and partitions distribution. Workers in their turn are the executors of the processing logic on the vertices assigned to them by the master.
Technically the processing logic applies on a vertex level. Theoretically, each vertex can contact any other vertex in the graph. To do that it must only know the id of the targeted object. In practice, this choice is often limited to the nearest neighbors of the vertex because of much smaller complexity. Once applied, the processing logic can change vertex state. If it happens, the new state can be sent to other vertices as a message. Messages exchange occurs in an iteration called superstep. In each of them, the vertex can access only to the message from the previous superstep. The iteration terminates when all active vertices were called.
In "Thinking Like a Vertex: A Survey of Vertex-Centric Frameworks for Large-Scale Distributed Graph Processing" paper (link in "Read also" section) the authors propose 4 main pillars of vertex-centric graph processing:
- Partitioning - specifies the strategy of splitting the vertices of the processed graph. Partitioning a graph is quite challenging because of Power Law explained in the previous post Graphs and data processing. It's very important to provide a good partitioning because very often a bad one will negatively impact the processing and especially the network traffic required to exchange the messages between vertices.
- Communication - tells how the vertices share the data. Two strategies exist here. The first one uses messages. A message contains local vertex data and is addressed to the worker holding the vertex partition. Later the worker decides where to send the message - locally, if the destination vertex is located on a local partition, or remotely if the vertex is on another machine.
Another communication strategy uses shared memory. It gets rid of message intermediary but on the other side adds much more complexity in distributed environments, especially because of concurrency. - Timing - determines the scheduling flow. It can be synchronous or asynchronous. Synchronous mode executes processing code on a given node only once in the supertep iteration. The execution of this iteration terminates only when it reaches a synchronization barrier. That happens when all vertices execute the processing logic within given iteration. Once it occurs the messages are exchanged, some vertices states are modified and a new iteration can start. This approach has some drawbacks, as costly coordination in terms of computation and the risk of stragglers (vertices taking much time to finish than others) that will slow down the whole iteration.
It's why an alternative approach in the form of asynchronous execution exists. It doesn't have the synchronization barrier and thanks to that any active vertex is available for new computation if resources are available. The scheduler can also do some optimization, as dynamically adapt the schedule to avoid stragglers impact. However, this model has more complexity than the previous one. Often it uses shared memory as the communication method that, as told, is hard to do well in distributed environment. Moreover, its flexibility, even though often optimizes the processing, sometimes can slow it down by applying much more updates than necessary to a vertex. - Execution model - defines program implementation and data flow. It's detailed better in the 3rd section because it directly impacts the data processing logic.
The key point of vertex-centric program is the a user-defined function specifying processing applied on each vertex. Usually, the function takes as parameters: vertex data, data of adjacent vertices and incoming edges. Its result can be propagated across outgoing edges to neighboring vertices. The function executes on each vertex as long as the latter remains in the active state. When all vertices become inactive or, as told, some threshold or the number of desired executions was reached, the computation terminates.
Usually the fault tolerance is provided with checkpointing. The graph is copied to some persistent storage (e.g. DFS) and in case of failure, it rollbacks to the most recent persisted state. The processing restarts from that point. But the checkpointing is not a single fault tolerance mechanism. The other systems can be based on the implementation framework. As an example we can take Apache Spark GraphX that uses Apache Spark's ability to lineage recovery from defined operations.
Execution models
The computational models are divided regarding their number of phases. The simplest model is called single phase and it represents the initial implementation of vertex-centric programs. In this case, the user-defined function does 3 things: accesses input data, computes a new value for the vertex and propagates the update to the rest of vertices by iterating over vertex outgoing edges. This method is easy to implement and was chosen for the first vertex-centric implementation - Google's Pregel. This framework uses the ideas from Bulk Synchronous Parallel (BSP), such as supersteps (BSP's components), network communication for messaging and synchronization barrier. Unlike classical BSP approach, Pregel introduces the state of vertices. In each superstep a vertex can be active or inactive. And this state is one of the halt conditions - when all vertices are inactive, the program stops.
Another execution model is two-phase model also called Scatter-Gather. This second name gives a lot of information about the 2 phases. The first one called scatter distributes the value of given vertex to its outgoing edges. The second stage, gather, collects the input message and applies it to the user-defined function. As a result of this operation, a vertex may update its local value and trigger scatter stage to send it to other vertices. This approach is met very often in the vertex-centric systems reading/writing data to/from edges. Among the implementations of Scatter-Gather, we can find one that lets the user define 2 processing functions. One of them is executed on each vertex in active subset. Another one applies on all outgoing edges in this subset. In this context, the subset is a view of the graph stored in a given partition.
The last execution model is three-phase model also known as Gather-Apply-Scatter. Sometimes another, extended, name is used: Gather-Sum-Apply-Scatter. One of its famous implementations is Apache Spark GraphX. As for the previous model, its logic is also defined in the second name. The execution consists of 3 steps. The first one, gather, an user-defined function is applied to each of adjacent edges for all vertices. The edge stores the values for edge's source and destination vertices. Later these values are passed to another function that reduces them into a single value, like in Map/Reduce. This operation corresponds to the sum stage in the 3rd used name that is sometimes omitted and included directly in gather. The result of this aggregation is sent to another data processing function executed in the apply phase. Here the result of the function sets a new vertex state. Finally, in scatter phase, another function executes for all edges that know the new values for source and destination vertices. In some implementations scatter phase is omitted. For instance, it's the case of Gelly that defines one of its computation models as Gather-Sum-Apply.
Vertex-centric example with Gelly
To see vertex-centric examples we'll use Apache Flink graph library called Gelly. It provides pretty clear interface for all of 3 listed execution models. But before showing the code, let's discover the tested graph:
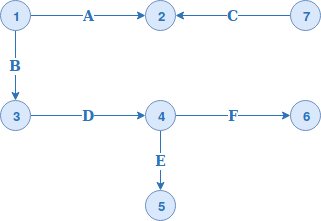
The single phase model in Gelly can be implemented as:
public class OnePhaseModelTest {
private static class ReceivedMessagesConcatenator extends MessageCombiner<Long, String> {
@Override
public void combineMessages(MessageIterator<String> contentWithNumberMessages) {
String sum = "";
while (contentWithNumberMessages.hasNext()) {
String receivedMessage = contentWithNumberMessages.next();
sum += receivedMessage;
}
sendCombinedMessage(sum);
}
}
private static class EdgesProcessor extends ComputeFunction<Long, String, String, String> {
@Override
public void compute(Vertex<Long, String> vertex,
MessageIterator<String> messageIterator) {
TestedGraph.Counter.ONE_PHASE.setExecution(getSuperstepNumber());
String valueFromMessages = "";
while (messageIterator.hasNext()) {
valueFromMessages += messageIterator.next();
}
if (!valueFromMessages.isEmpty() || isTrunk(vertex)) {
String value = valueFromMessages;
getEdges().forEach(edge -> {
String valueToSend = value+edge.getValue();
sendMessageTo(edge.getTarget(), valueToSend);
});
}
setNewVertexValue(TestedGraph.lettersToSorted(vertex.getValue() + valueFromMessages));
}
private boolean isTrunk(Vertex<Long, String> vertex) {
return vertex.getId() == 1L || vertex.getId() == 7L;
}
}
@Test
public void should_traverse_graph_and_accumulate_edge_values() throws Exception {
// Just for simpler debugging, set the parallelism level to 1
VertexCentricConfiguration configuration = new VertexCentricConfiguration();
configuration.setParallelism(1);
Graph<Long, String, String> graph = TestedGraph.getGraph();
// We define here a big number of iterations
// At the end we'll see whether Gelly really computed the value in 20 iterations
int maxIterations = 20;
Graph<Long, String, String> result = graph.runVertexCentricIteration(new EdgesProcessor(),
new ReceivedMessagesConcatenator(), maxIterations, configuration);
List<Vertex<Long, String>> updatedVertices = result.getVertices().collect();
assertThat(updatedVertices).containsAll(Arrays.asList(
new Vertex<>(2L, "AC"), new Vertex<>(1L, ""), new Vertex<>(3L, "B"), new Vertex<>(7L, ""),
new Vertex<>(6L, "BDF"), new Vertex<>(5L, "BDE"), new Vertex<>(4L, "BD")
));
assertThat(TestedGraph.Counter.ONE_PHASE.get()).isEqualTo(4);
}
}
public class TestedGraph {
public static Graph<Long, String, String> getGraph() {
ExecutionEnvironment env = ExecutionEnvironment.getExecutionEnvironment();
List<Edge<Long, String>> edges = Arrays.asList(new Edge<>(1L, 2L, "A"), new Edge<>(1L, 3L, "B"),
new Edge<>(3L, 4L, "D"), new Edge<>(4L, 5L, "E"), new Edge<>(4L, 6L, "F"), new Edge<>(7L, 2L, "C")
);
List<Vertex<Long, String>> vertices = Arrays.asList(new Vertex<>(1L, ""), new Vertex<>(2L, ""),
new Vertex<>(3L, ""), new Vertex<>(4L, ""), new Vertex<>(5L, ""), new Vertex<>(6L, ""), new Vertex<>(7L, "")
);
return Graph.fromCollection(vertices, edges, env);
}
public static String lettersToSorted(String lettersToSort) {
List<String> letters = Arrays.asList(lettersToSort.split(""));
letters.sort(Comparator.naturalOrder());
return String.join("", letters);
}
public enum Counter {
ONE_PHASE(new AtomicInteger(0)),
TWO_PHASES(new AtomicInteger(0)),
THREE_PHASES(new AtomicInteger(0));
private AtomicInteger executions;
Counter(AtomicInteger executions) {
this.executions = executions;
}
public void setExecution(int nr) {
executions.set(nr);
}
public int get() {
return executions.get();
}
}
}
The following table summarizes the execution steps for a single phase processing:
| Superstep | What happens |
|---|---|
| 1 | All vertices are active but only root ones send messages with edge values to their neighbours: (1)-[A]->(2), (7)-[C]->(2) and (1)-[B]->(3). |
| 2 |
All vertices update their states with received messages. Hence (2) => "AC" and (3) => B. In this superstep only updated vertices are active. Since only (3) has outgoing edges, it sends (3)-[BD]->(4) |
| 3 | Vertice (4) receives the message and updates its state: (4) => "BD". It has 2 outgoing edges and sends these 2 messages: (4)-[BDE]->(5) and (4)-[BDF]->(6) |
| 4 | Vertices (5) and (6) receive the messages and update their states to: (B) => "BDE" and (6) => "BDF" |
Two phase model decouples the logic of accumulate values from the one of updating them:
public class TwoPhaseModelTest {
@Test
public void should_traverse_graph_and_accumulate_edge_values() throws Exception {
// Just for simpler debugging, set the parallelism level to 1
VertexCentricConfiguration configuration = new VertexCentricConfiguration();
configuration.setParallelism(1);
Graph<Long, String, String> graph = TestedGraph.getGraph();
// We define here a big number of iterations
// At the end we'll see whether Gelly really computed the value in 20 iterations
int maxIterations = 20;
Graph<Long, String, String> result = graph.runScatterGatherIteration(new Scatter(), new Gather(), maxIterations);
List<Vertex<Long, String>> updatedVertices = result.getVertices().collect();
assertThat(updatedVertices).containsAll(Arrays.asList(
new Vertex<>(2L, "AC"), new Vertex<>(1L, ""), new Vertex<>(3L, "B"), new Vertex<>(7L, ""),
new Vertex<>(6L, "BDF"), new Vertex<>(5L, "BDE"), new Vertex<>(4L, "BD")
));
assertThat(TestedGraph.Counter.TWO_PHASES.get()).isEqualTo(4);
}
private static class Scatter extends ScatterFunction<Long, String, String, String> {
@Override
public void sendMessages(Vertex<Long, String> vertex) throws Exception {
TestedGraph.Counter.TWO_PHASES.setExecution(getSuperstepNumber());
// In the 1st superstep all vertices are considered as active
// It's why here we process only trunks. Trunks trigger 1st level children that, in their turn, trigger
// 2nd level children and so on. It explains why we can have a control on superstep number
// It's only a little bit wasteful to have to filter trunks - it would be good to specify "starting nodes"
// before executing the query
if (isTrunk(vertex) || getSuperstepNumber() != 1) {
for (Edge<Long, String> edge : getEdges()) {
sendMessageTo(edge.getTarget(), vertex.getValue()+edge.getValue());
}
}
}
private boolean isTrunk(Vertex<Long, String> vertex) {
return vertex.getId() == 1 || vertex.getId() == 7;
}
}
private static class Gather extends GatherFunction<Long, String, String> {
@Override
public void updateVertex(Vertex<Long, String> vertex, MessageIterator<String> inMessages) throws Exception {
String newValue = "";
while (inMessages.hasNext()) {
newValue += inMessages.next();
}
setNewVertexValue(TestedGraph.lettersToSorted(vertex.getValue() + newValue));
}
}
}
And in summary it gives:
| Superstep | Scatter | Gather |
|---|---|---|
| 1 | All vertices are active but only root ones send messages with edge values to their neighbours: (1)-[A]->(2), (7)-[C]->(2) and (1)-[B]->(3). | Vertices (2) and (3) handle messages sent by (1) and (7). Their update states are: (2) => "AC" and (3) => "B". |
| 2 | Only updated vertices are active. Since only (3) has outgoing edges, it sends (3)-[BD]->(4) | Vertex (4) updates its state to (4) => "BD". |
| 3 | Active vertex (4) has 2 outgoing edges and sends these 2 messages: (4)-[BDE]->(5) and (4)-[BDF]->(6) | Vertices (5) and (6) update their states: (5) => "BDE" and (6) => "BDF" |
| 4 | The 2 last active vertices (5) and (6) don't have outgoing edges. They don't send message. | - |
Finally, the model based on 3 steps adds a combiner stage:
public class TreePhaseModelTest {
@Test
public void should_traverse_graph_and_accumulate_edge_values() throws Exception {
// Just for simpler debugging, set the parallelism level to 1
VertexCentricConfiguration configuration = new VertexCentricConfiguration();
configuration.setParallelism(1);
Graph<Long, String, String> graph = TestedGraph.getGraph();
// We define here a big number of iterations
// At the end we'll see whether Gelly really computed the value in 20 iterations
int maxIterations = 20;
Graph<Long, String, String> result = graph.runGatherSumApplyIteration(new Gather(),
new Sum(), new Apply(), maxIterations);
List<Vertex<Long, String>> updatedVertices = result.getVertices().collect();
assertThat(updatedVertices).containsAll(Arrays.asList(
new Vertex<>(2L, "AC"), new Vertex<>(1L, ""), new Vertex<>(3L, "B"), new Vertex<>(7L, ""),
new Vertex<>(6L, "BDF"), new Vertex<>(5L, "BDE"), new Vertex<>(4L, "BD")
));
assertThat(TestedGraph.Counter.THREE_PHASES.get()).isEqualTo(3);
}
private static class Gather extends GatherFunction<String, String, String> {
@Override
public String gather(Neighbor<String, String> neighbor) {
TestedGraph.Counter.THREE_PHASES.setExecution(getSuperstepNumber());
return neighbor.getNeighborValue() + neighbor.getEdgeValue();
}
}
private static class Sum extends SumFunction<String, String, String> {
@Override
public String sum(String value1, String value2) {
// It's invoked only when there are more than 1 value returned by gather step
return value1 + value2;
}
}
private static class Apply extends ApplyFunction<Long, String, String> {
@Override
public void apply(String newValue, String currentValue) {
// It's called at the end for every active vertex
// When the value is really updated, i.e. it's different from the previous value, the updated vertex
// remains active and its neighbors are invoked in the next superstep
// Here, only for testing, we sort the values to get always the same results (sometimes A and C are inversed)
this.setResult(TestedGraph.lettersToSorted(newValue));
}
}
}
And in summary it gives:
| Superstep | Gather | Sum | Apply |
|---|---|---|---|
| 1 | All vertices are active but here the edges are collected and sent to destination vertices. | Only vertex (2) received more than 1 message. Its 2 messages are combined here into a single one: "A" + "C" = "AC" | Reduced messages are applied on edges destination vertices: (2) => "AC", (3) => "B", (4) => "D", (5) => "E", (6) => "F". |
| 2 | All 4 updates vertices having outgoing edges are active. New values of (3)->(4), (4)->(5) and (4)->(6) are gathered. | This operation is not executed. There is no a vertex with 2 or more messages. | New values are set to: (4) => "BD", (5) => "DE", (6) => "DF" |
| 3 | Remaining 3 updated vertieces are active. Messages (4)->(5) and (4)->(6) are sent once again but with different values. | Not executed, each vertex has 1 message. | Vertices (5) and (6) update their states: (5) => "BDE" and (6) => "BDF" |
This post presented vertex-centric graph processing. As the name suggests, it's based on iterative execution of the user-defined functions of partitioned vertices. Most often the updated data is sent through messages but, as explained in the 4-pillars list, it's also possible to use shared memory. The execution is synchronous, with a synchronization barrier at the end of each iteration called superstep. However, an asynchronous version exists. It's more difficult to implement though. The vertex-centric concept can be made with one of 3 execution models: 1 phase, 2 phases and 3 phases. They differentiate by the number of user-defined functions. In the former, only 1 function is defined. It does both: sending messages and updating vertex value. Two other versions use more functions, as I presented that in the last section with a traversal-like example and more random-access one.
