Previously described vertex-centric model is not the single one used to process graph data. Another one uses subgraphs as the processing unit.
This post talks about graph-centric graph processing. Its first section presents the "why" and "how" of its existence. Next one shows the main concept that should implement any graph-centric framework. The third one talks more about the partitioning in such kind of processing. Finally, the last section discusses one of the implementations of graph-centric approach, GoFFish. Please notice that the graph-centric term is used interchangeably with sub-graph centric. This post will use the former version.
Generally about graph-centric approach
Just to recall quickly, vertex-centric approach applies at vertex level either until the moment where no new updates are generated or a maximal number of iterations is reached. This brings scalability but also some issues. One of them is the time needed to propagate updates between vertices. Since the framework operates by single hops in iterations called supersteps, sometimes it may take time to communicate with targeted node. Moreover, communication comes with the cost of network messaging and if we have a lot of big messages to exchange, it may become problematic too.
Graph-centric approach addresses the issues of communication latency by proposing another data structure for further processing. Instead of storing different vertices on each partition it proposes to store there subgraphs. Of course, it doesn't come without communication requirement but it's much smaller if the graph is well partitioned since the communication occurs locally inside the partition.
Implementation details
The whole idea looks nice but what are its implementation details? First of all, the graph is partitioned into smaller subgraphs. Each of them contains vertices that sometimes can be duplicated across two or more partitions. Such duplicated vertices are called boundary vertices. The primary representation is always owned by a single partition. Boundary vertex contains only a value coming one particular superstep of the computation.
Another type of vertices is called internal vertex. Such vertex has all information about itself and adjacent edges. An internal vertex is also a special form of boundary vertex. It's a boundary vertex located on the owner partition. There is always one owner of each vertex and as told, the others are just its local copies. It emphasizes the fact of good partitioning because all updated information must be replicated every time on boundary vertices.
The data processing itself uses the single-, two- and three- phase concepts described in the post about Vertex-centric graph processing. However, the difference is that most of the messages are exchanges inside the partition. The exception for that rule are boundary vertices. Any update they make must be propagated to their internal vertex at the end of each superstep. Internal vertices process later these propagated updates. Since the processing can involve update value modification, the results may be sent back to the boundary vertices before the beginning of new superstep. But this behavior if left to the implementation. Regarding internal vertices and depending on the final implementation, the algorithm can modify the value of any internal vertice without sending it through the network and waiting for new superstep to begin.
Graph-centric and partitioning
A good graph-centric partitioning strategy should minimize the number of edges connecting different partitions. This property is called ncut and keeping it small helps to reduce the partition to partition communication overhead. The most simplistic partitioning approach uses randomly hashed vertices. Unfortunately, it doesn't provide a good ncut ratio. As presented in "From "Think Like a Vertex" to "Think Like a Graph" paper, it often leads to a big overhead when 97-99% of vertices will need to communicate !
The researches of the quoted paper (link in Read also section) propose another solution based on graph coarsening. Its idea summarizes in the following image:
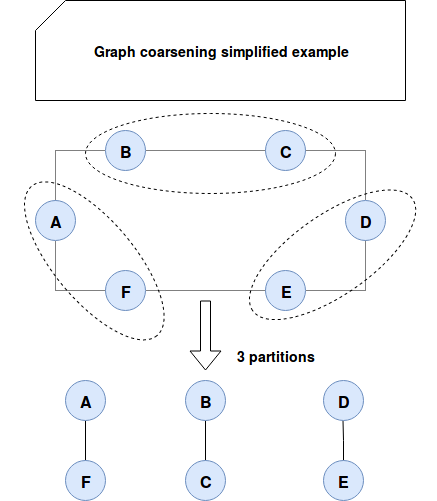
As you can see, the graph first is coarsed, i.e. divided into smaller parts that can easily fit into a single machine. Later such decomposed graph is parittioned with the goal to avoid too many edge-cuts on different partitions. Finally, the third step called uncoarsing projects partitions back to the original graph. The whole process looks similar to compressing a set of files, distributing them evenly on different nodes and uncompressing them. In the datasets from the paper, this algorithm reduced ncut property to only 2-7%.
Unfortunately the coarse-based partitioning is not the optimal solution because, still according to the paper, it leads to unbalanced partitions. However, producing balanced partitions and keeping minimal communication cost at the same time is an NP-hard problem.
GoFFish implementation
GoFFish is one of the implementations of graph-centric processing framework. Why this choice? Initially, I wanted to illustrate the post with Giraph++ or NSpark projects described in some of the scientific papers. But I didn't find the source code for them. It wasn't the case of GoFFish that has the code available on GitHub - even though the last update comes from 2017 and the source still has a lot of TODOs.
The framework is composed of 2 main parts: a distributed storage engine called Graph oriented File System (GoFs) and a processing engine called Gopher execution engine. The implementation uses a master-slave architecture where worker nodes execute the processing code and the master monitors the progress. The workers load their subgraphs into memory. The execution consists of calling the Compute function in every superstep. At the end of each iteration, the worker can send a message to boundary vertices. The computation terminates when all workers sent the ready to halt message. It means that there are no active subgraphs.
Internally GoFFish implementation for Giraph provides some abstractions specific for subgraph-centric approach. in.dream_lab.goffish.api.ISubgraph interface represent the subgraph stored in memory by each worker and processed iteratively in supersteps. The subgraph is composed of local and remote vertices. It also has a method returning subgraph edges. The communication with boundary vertices is delegated to Giraph's AbstractComputation class and its WorkerClientRequestProcessor instance. The computation terminates when all subgraphs invoked voteToHalt() method.
Graph-centric approach seems to get less popularity than vertex-centric paradigm. We can deduce that after available implementations where among quoted Giraph++, NSpark and GoFFish, only the latter one was published. And despite that, we can keep in mind this idea of subgraphs. It can be more or less easily implemented with the help of data processing frameworks as Apache Spark and not distributed graph databases like Neo4j. The whole idea was explained in the post Neo4j scalability and Apache Spar. However, it doesn't go so far as the pure graph-centric concept which addresses not only distributed processing but also the problem of good partitioning and synchronization between subgraphs.
