One of important characteristics of distributed graph processing which makes it different from classical Map/Reduce approach is the iterative nature of many algorithms. Pregel is one of the computation models that supports such kind of processing very well, while Apache Spark GraphX comes with its own Pregel implementation.
In this next post from Apache Spark GraphX series we'll discover iterative algorithms with Pregel operator. The first section provides us with its thorough description, together with some internal details. The next one shows the execution flow of a simple iterative algorithm. The last section presents some specific implementations of several popular iterative algorithms.
Pregel operator
Pregel is one of the most popular implementation of vertex-centric graph processing. If you're interested in more details, I recommend reading the linked post. The most important concepts of the following approach is the fact that:
- It's iterative - each iteration is called a supertstep. The iterations stop when some threshold or the maximal number of iterations is reached.
- It's message-based - in each iteration the vertices communicate with their neighbors. A vertex can be in active or inactive state. In the former one it was sending the messages. A vertex can become inactive when its value doesn't change in a given iteration.
- It has an update function - each vertex accumulates the messages from its nearest neighbors. At the end it applies a reduce function on them to compute its new value. If the value changes, it propagates it to its neighbors in the next superstep.
GraphX provides an implementation of such processing that it's different from the original one. Unlike the initial Pregel API specification, GraphX's one lets the exchanged messages access the attributes of both - source and destination - vertices. In addition to that, GraphX uses a reduce approach, i.e. it doesn't need to wait for all messages to be received by each vertex to begin the computation of its new value. Instead it computes them partially on each partition and merges into the final value at the end.
The Pregel computation on GraphX applies to the triplet and we can see that every time when the new set of messages is computed:
var messages = GraphXUtils.mapReduceTriplets(g, sendMsg, mergeMsg)
A quick analysis of org.apache.spark.graphx.Pregel shows the presence of a feature already discussed in the GraphX and fault-tolerance . As the name suggests, PeriodicGraphCheckpointer checkpoints the computed graph periodically. It was created because of the initial lack of support for long lineage chains created by iterative algorithms. In this context the RDDs are created very often after dozens or even hundreds of iterations that sometimes led to StackOverflowExceptions.
Execution flow
The execution flow of Pregel-based GraphX program can be summarized in the following big picture schema:
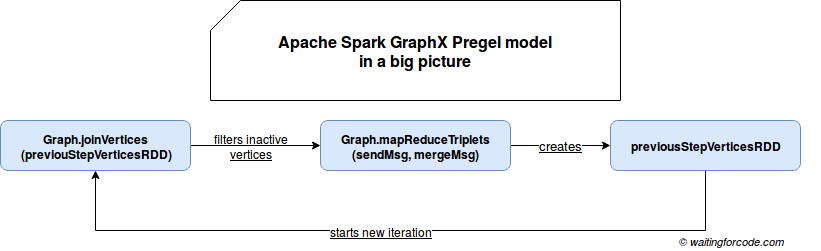
In the picture you can see that the iteration is composed of 2 major steps. The former one consists on calling Graph's joinVertices[U: ClassTag](table: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, U) => VD) which applies mapFunc for every vertices pair present in both RDDs. If the vertex is not present in the joined RDD, it keeps its old value. The role of this processing block is to compute new value of the vertex with the messages aggregated in the previous iteration.
Another block requires a little bit more detailed analysis. It can be divided into the following subblocks:
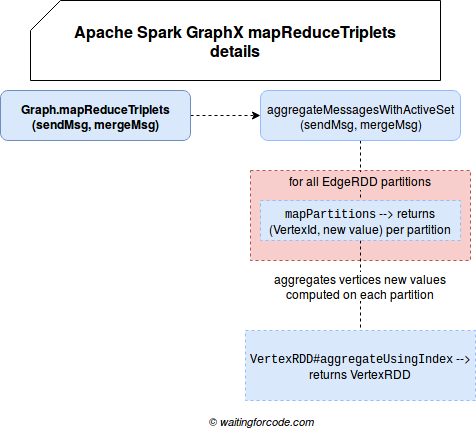
The exchange of messages is a little bit more complicated than the computation of new values in vertices. It delegates the computation to aggregateMessagesWithActiveSet[A: ClassTag](sendMsg: EdgeContext[VD, ED, A] => Unit, mergeMsg: (A, A) => A, tripletFields: TripletFields, activeSetOpt: Option[(VertexRDD[_], EdgeDirection)]) method which, as you can see, takes some interesting parameters:
- sendMsg: EdgeContext[VD, ED, A] => Unit - it defines the method responsible for sending the message to vertices neighbors. It takes the sendMsg function defined for the Pregel program and wraps it with another function taking an EdgeContext instance as parameter. This context object has the information about the computed triplets so apart from a source and a target ids, it also knows the attributes of both vertices. The wrapped function generates a pair of (VertexId, Message) and the wrapper defines the communication logic and sends the message either to the source or to destination vertex.
- mergeMsg: (A, A) => A - it's the reducer responsible for taking the messages generated for the same vertex at the partition level and computing a single value. It considerably reduces the communication overhead if given partition contains a lot of edges of one specific vertex.
- tripletFields: TripletFields - defines the fields to include in the EdgeContext passed to the sendMsg's wrapper function.
- activeSetOpt: Option[(VertexRDD[_], EdgeDirection)]) - this is where the "filtering" of inactive vertices happens. Under-the-hood the aggregate MessagesWithActiveSet calls org.apache.spark.graphx.impl.ReplicatedVertexView#withActiveSet method which disables the vertices not defined in the activeSetOpt's RDD.
The whole iteration of GraphX Pregel proceeds as follows:
while (activeMessages > 0 && i < maxIterations) {
// Receive the messages and update the vertices.
prevG = g
g = g.joinVertices(messages)(vprog)
graphCheckpointer.update(g)
val oldMessages = messages
// Send new messages, skipping edges where neither side received a message. We must cache
// messages so it can be materialized on the next line, allowing us to uncache the previous
// iteration.
messages = GraphXUtils.mapReduceTriplets(
g, sendMsg, mergeMsg, Some((oldMessages, activeDirection)))
// The call to count() materializes `messages` and the vertices of `g`. This hides oldMessages
// (depended on by the vertices of g) and the vertices of prevG (depended on by oldMessages
// and the vertices of g).
messageCheckpointer.update(messages.asInstanceOf[RDD[(VertexId, A)]])
activeMessages = messages.count()
logInfo("Pregel finished iteration " + i)
// … checkpointing activity
// count the iteration
i += 1
}
GraphX Pregel example
To see GraphX's Pregel in action we'll use the following graph structure:
private val vertices = testSparkContext.parallelize(
Seq((1L, ""), (2L, ""), (3L, ""), (4L, ""), (5L, ""))
)
private val edges = testSparkContext.parallelize(
Seq(Edge(1L, 2L, 10), Edge(2, 3, 15), Edge(3, 5, 0), Edge(4, 1, 3))
)
private val graph = Graph(vertices, edges)
// The tested graph looks like:
// (1)-[value: 10]->(2)-[value: 15]->(3)-[value: 0]->(5)
// ^
// |
// [value: 3]
// |
// (4)
As you can see, the tested graph is quite simple. So is the processing functions:
object PregelFunctions {
val IteratedPaths = new scala.collection.mutable.ListBuffer[String]()
def mergeMessageBeginningSuperstep(vertexId: Long, currentValue: String, message: String): String = {
message
}
def mergeMessagePartitionLevel(message1: String, message2: String) = s"${message1} + ${message2}"
def createMessages(edgeTriplet: EdgeTriplet[String, Int]): Iterator[(VertexId, String)] = {
val resolvedMessage = if (edgeTriplet.srcAttr.trim.isEmpty) {
edgeTriplet.attr.toString
} else {
edgeTriplet.srcAttr + " + " + edgeTriplet.attr.toString
}
IteratedPaths.synchronized {
IteratedPaths.append(edgeTriplet.toString())
}
Iterator((edgeTriplet.dstId, resolvedMessage))
}
}
The functions concatenate the values of adjacent neighbors. The value of each vertex will be the path to that vertex from the root (vertex with id 4). Let's start by checking the stop conditions with the maximal number of iterations or inactive vertices:
it should "stop iteration after reaching the maximal number of iterations" in {
val graphWithPathVertices = Pregel(graph, "", 2,
EdgeDirection.In)(PregelFunctions.mergeMessageBeginningSuperstep, PregelFunctions.createMessages,
PregelFunctions.mergeMessagePartitionLevel)
val verticesWithAttrs = graphWithPathVertices.vertices.collectAsMap()
verticesWithAttrs should have size 5
verticesWithAttrs should contain allOf((2, "3 + 10"), (5, "15 + 0"), (4, ""), (1, "3"), (3, "10 + 15"))
}
it should "stop iteration when no more vertices are active" in {
val graphWithPathVertices = Pregel(graph, "", 10,
EdgeDirection.In)(PregelFunctions.mergeMessageBeginningSuperstep, PregelFunctions.createMessages,
PregelFunctions.mergeMessagePartitionLevel)
val verticesWithAttrs = graphWithPathVertices.vertices.collectAsMap()
verticesWithAttrs should have size 5
verticesWithAttrs should contain allOf((2, "3 + 10"), (5, "3 + 10 + 15 + 0"), (4, ""), (1, "3"), (3, "3 + 10 + 15"))
}
Even though the results are correct right now, the tests weren't easy because initially I ignored the direction parameter (EdgeDirection.In). And in fact it's the key to detect whether a vertex can be still an active member of the iteration or not. The EdgeDIrection.In value means that only the vertices which received a message in previous iteration are still active. It fits pretty fine in path-reconstruction test. But the "in" direction is not the single one. Its opposite is "out", and 2 more constrained are EdgeDirection.Either and EdgeDirection.Both:
behavior of "direction parameter"
it should "send a message to the vertices that received the message in both sides of the edge" in {
val graphWithPathVertices = Pregel(graph, "", 10,
EdgeDirection.Both)(PregelFunctions.mergeMessageBeginningSuperstep, PregelFunctions.createMessages,
PregelFunctions.mergeMessagePartitionLevel)
val verticesWithAttrs = graphWithPathVertices.vertices.collectAsMap()
verticesWithAttrs should have size 5
verticesWithAttrs should contain allOf((2, "3 + 10"), (5, "3 + 10 + 15 + 0"), (4, ""), (1, "3"), (3, "3 + 10 + 15"))
PregelFunctions.IteratedPaths should have size 10
PregelFunctions.IteratedPaths.contains("((4,),(1,3),3)") shouldBe false
}
it should "send a message to the vertices that received the message in at least one side of the edge" in {
val graphWithPathVertices = Pregel(graph, "", 10,
EdgeDirection.Either)(PregelFunctions.mergeMessageBeginningSuperstep, PregelFunctions.createMessages,
PregelFunctions.mergeMessagePartitionLevel)
val verticesWithAttrs = graphWithPathVertices.vertices.collectAsMap()
verticesWithAttrs should have size 5
verticesWithAttrs should contain allOf((2, "3 + 10"), (5, "3 + 10 + 15 + 0"), (4, ""), (1, "3"), (3, "3 + 10 + 15"))
PregelFunctions.IteratedPaths should have size 44
PregelFunctions.IteratedPaths should contain allOf("((4,),(1,),3)", "((4,),(1,3),3)")
PregelFunctions.IteratedPaths.groupBy(path => path)("((4,),(1,3),3)") should have size 10
}
Even though the direction doesn't impact the final results in our case, it impacts the performance of the processing. As you can see in above 2 test cases, the number of iterations is much bigger for the edges whose one of vertices received a message.
Apache GraphX implements Pregel-based iterative computation with some extra changes. The most important one is the checkpoint mechanism that avoids StackOverflow exceptions. The implementation also provides bigger parallelism through partial aggregations at partitions levels. It also has a possibility to configure the criterion for active vertices with the direction parameter. As we saw in the 3rd section, this parameter impacts the number of iterations, that is why, if used inappropriately, it can slow down the whole processing.
